lazyivy
lazyivy is a Rust crate that provides tools to solve initial value problems of
the form dY/dt = F(t, Y) using Runge-Kutta methods, where Y is a vector
and t is a scalar.
The algorithms are implemented using the struct RungeKutta, that implements
Iterator. The following Runge-Kutta methods are implemented currently, and
more will be added in the near future.
- Euler 1
- Ralston 2
- Huen-Euler 2(1)
- Bogacki-Shampine 3(2)
- Fehlberg 4(5)
- Dormand-Prince 5(4)
(p is the order of the method and (p*) is the order of the embedded
error estimator, if it is present.)
Lazy integration
RungeKutta implements the Iterator trait. Each .next() call advances the
iteration to the next Runge-Kutta step and returns a tuple (t, Y), where
t is the dependent variable and Y is Array1<f64>.
Note that each Runge-Kutta step contains s number of internal stages.
Using lazyivy, there is no way at present to access the integration values for
these inner stages. The .next() call returns the final result for each step,
summed over all stages.
The lazy implementation of Runge-Kutta means that you can consume the iterator
in different ways. For e.g., you can use .last() to keep only the final
result, .collect() to gather the state at all steps, .map() to chain the
iterator with another, etc. You may also choose to use it in a for loop and
implement you own logic for modifying the step-size or customizing the stop
condition.
API is unstable. It is active and under development.
Usage:
After adding lazyivy to Cargo.toml, create an initial value problem using
the provided builder. Here is an example
showing how to solve the Brusselator.
\frac{d}{dt} \left[ \begin{array}{c}
y_1 \\ y_2 \end{array}\right] = \left[\begin{array}{c}1 - y_1^2 y_2 - 4 y_1
\\ 3y_1 - y_1^2 y_2 \end{array} \right]
use RungeKutta;
use ;
The result when plotted looks like this,
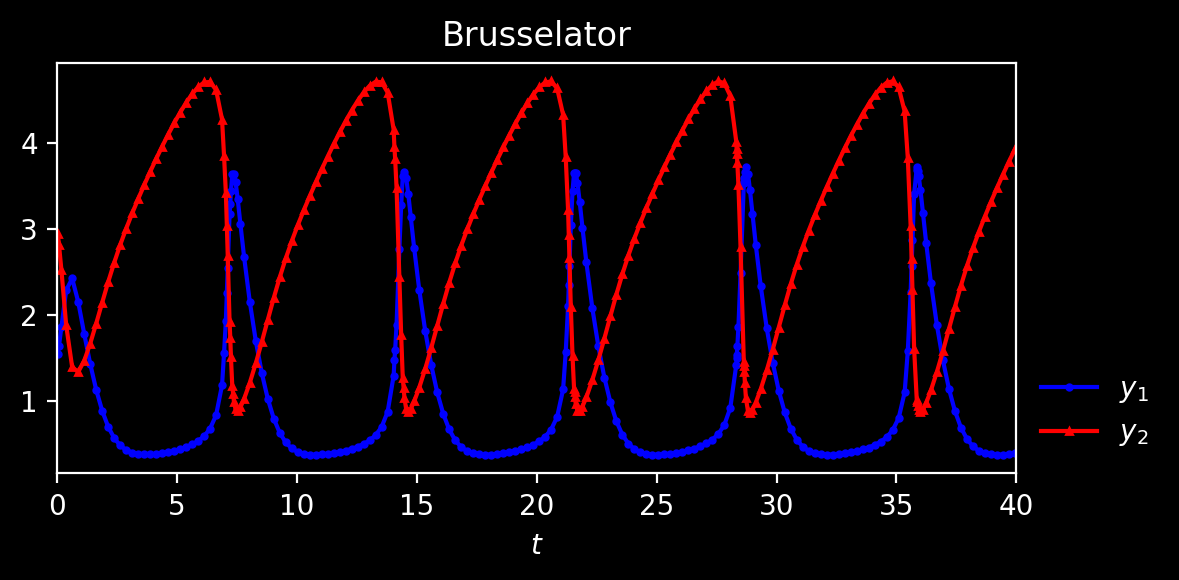
Likewise, you can do the same for other problems, e.g. for the Lorenz attractor, define the evaluation function
You can also use closures to capture the environment and wrap your evaluation. That is, if you have a function -
you cannot pass this to RungeKutta::builder() directly. But you can wrap this
into a closure. E.g.,
let sigma = 10.;
let beta = 8. / 3.;
let rho: 28.;
let eval_closure = ;
let integrator = builder
... // other parameters
.build;
This works because closures that do not modify their environments can coerce to
Fn. Hence, this pattern will not work for closures that mutate their
environments. In general, you can use any evaluation function and stop condition,
but they must be Fn(&f64, ArrayView1<f64>, ArrayViewMut1<f64>) and
Fn(&f64, ArrayView1<f64>) -> bool, respectively.
Here is a plot showing the Lorenz attractor result.
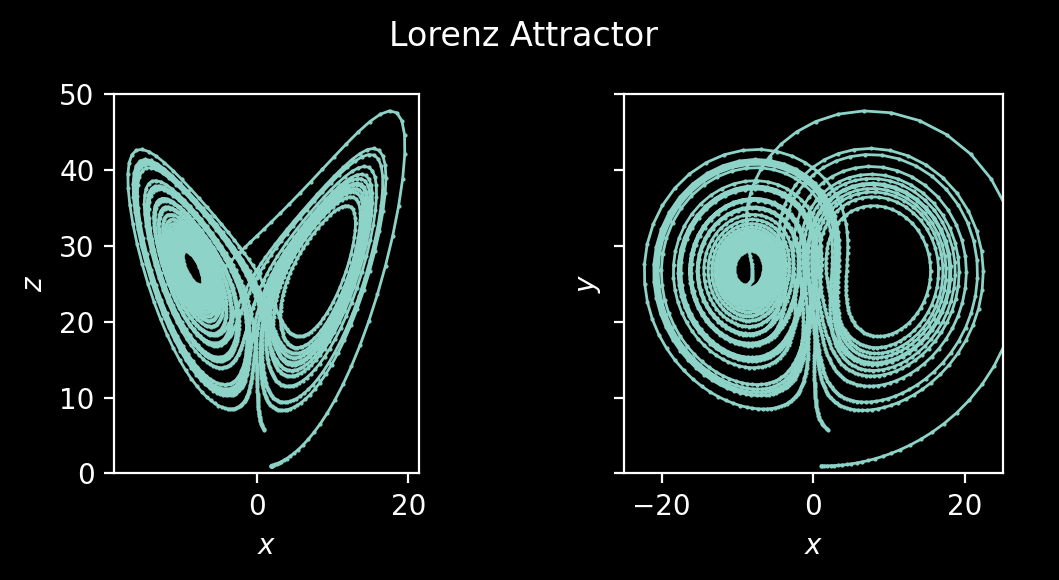
Mutating in-place (as of version 0.5.0)
In the above example for the Lorenz attractor, I created a new array using the
array! macro. However, I recommend in practice that you use evaluation
functions that mutate a result array that is passed to the function.
For example, the same example could take the form -
And then you can wrap this in a closure with the appropriate signature.
let sigma = 10.;
let beta = 8. / 3.;
let rho: 28.;
let eval_closure = ;
This way you will avoid an allocation each time the function is called.
To facilitate this change, as of v0.5.0, the signature of the generic parameter F
that was previously Fn(&f64, &Array1<f64>) -> Array1<f64> was changed to
Fn(&f64, ArrayView1<f64>, ArrayViewMut1<f64>).
Since Rust does not allow for mutiple mutable references, this change does mean
that RungeKutta is no longer thread-safe. But, this should be fine because
Runge-Kutta iterations are sequential and cannot easily be multi-threaded.
To-do:
- Add better tests.
- Benchmark.

