# Bend: a high-level parallel language
Bend is a massively parallel, high-level programming language. Unlike existing
alternatives like CUDA, OpenCL and Metal, which are low-level and limited, Bend
has the feel and features of a modern language like Python and Haskell. Yet, for
the first time ever, this language runs directly on GPUs, using
thousands of cores with 0 annotations, powered by the [HVM2](https://github.com/HigherOrderCO/hvm2).
HVM2 is the successor to HVM1, a 2022 prototype of this concept. Through the
last year, we put massive effort into polishing, simplifying, and verifying
HVM's correctness. As a result, we're now finally able to run it smoothly on
GPUs. It still has many limitations, but it is finally stable, production-ready,
and a solid foundation for all that is to come. HOC will provide long-term
support for all features listed on HVM2's whitepaper.
## Using Bend
Using Bend is simple. Just install it with:
//TODO
And then run `bend <file.bend>`.
## Examples
### Parallel Sum
In Bend, any work that can be done in parallel *will* be done in parallel, with
maximum granularity. For example, in `f(A) + g(B)`, both calls are independent,
so Bend will execute them in parallel. This gives us a very general way to
implement parallelism: via recursion. For example, the program below adds all
numbers from 0 to ~1 billion in a *parallelizable fashion*:
```
# Sums all numbers from 0 til 2^depth:
def sum(depth, x):
switch depth:
case 0:
return x
case _:
fst = sum(depth-1, x*2+0) # adds the fst half
snd = sum(depth-1, x*2+1) # adds the snd half
return fst + snd
def main:
return sum(30, 0)
```
Here is how it performs:
- CPU, Apple M3 Max, 1 thread: **3.5 minutes**
- CPU, Apple M3 Max, 16 threads: **10.26 seconds**
- GPU, NVIDIA RTX 4090, 32k threads: **1.88 seconds**
Of course, adding numbers recursively isn't the best use case for Bend, as you
could do it very fast with a low-level sequential loop. But not everything can
be done that way.
### Parallel Bitonic Sort
The Bitonic Sort algorithm is based on the following network:
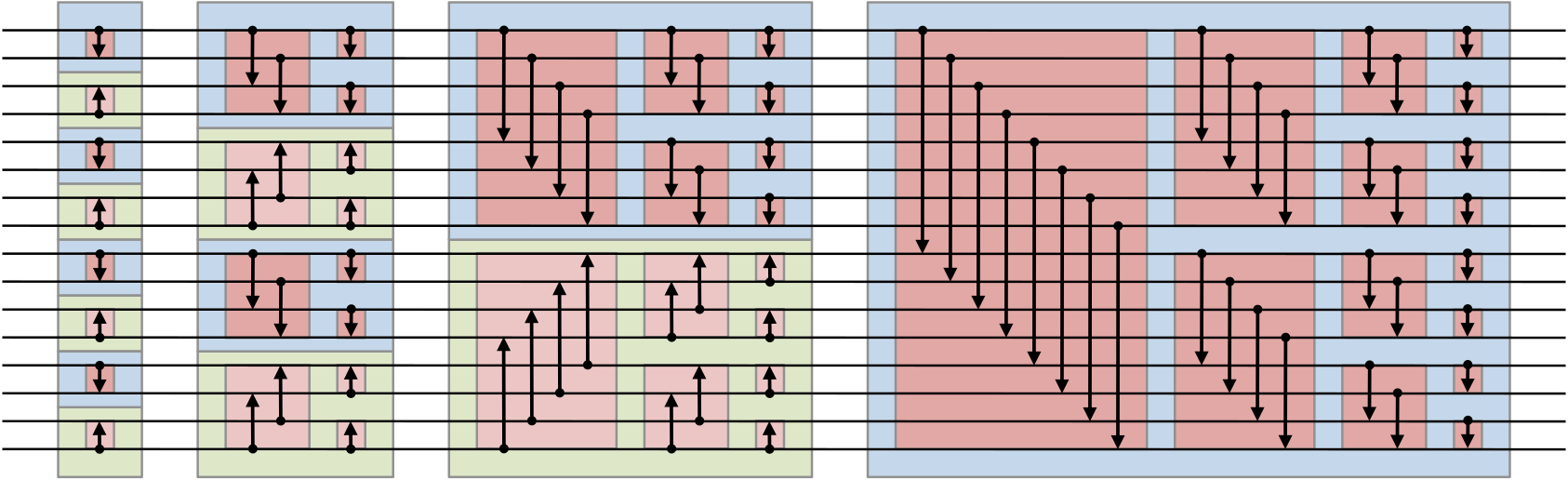
Basically, numbers "pass through" the network along its 16 horizontal wires.
Every time they reach two ends of an arrow, they're swapped to ensure that the
arrow points towards to largest. At the end, all numbers will be sorted!
Implementing a Bitonic Sort in C-like languages can be challenging, as it
involves coordination of shared memory accesses. A less known fact is that all
sorting algorithms can be described as a series of tree rotations. Bend supports
a functional style, allowing one to implement it with just 9 equations:
```
// Swaps distant values in parallel; corresponds to a Red Box
(warp s (Leaf a) (Leaf b)) = (U60.swap (^ (> a b) s) (Leaf a) (Leaf b))
(warp s (Node a b) (Node c d)) = (join (warp s a c) (warp s b d))
// Rebuilds the warped tree in the original order
(join (Node a b) (Node c d)) = (Node (Node a c) (Node b d))
// Recursively warps each sub-tree; corresponds to a Blue/Green Box
(flow s (Leaf a)) = (Leaf a)
(flow s (Node a b)) = (down s (warp s a b))
// Propagates Flow downwards
(down s (Leaf a)) = (Leaf a)
(down s (Node a b)) = (Node (flow s a) (flow s b))
// Bitonic Sort
(sort s (Leaf a)) = (Leaf a)
(sort s (Node a b)) = (flow s (Node (sort 0 a) (sort 1 b)))
```
Unlike the CUDA counterpart, this version of the algorithm is extremely
high-level, relying on millions of small allocations, tree rotations and
recursion. It isn't even possible to express it that way in any existing
GPU-targeting language. Bend is capable of compiling that algorithm, as is,
to in more than 32 thousand CUDA threads, achieving a near-ideal speedup:
... graphics or numbers here ...
### 3D Graphics
TODO: perhaps write a mendelbrot set renderer in Bend, render with the
DRAW_IMAGE IO, and measure the time it took, compared to, say, a sequential C
implementation?
## Limitations
- only 1 dup label
- no lazy mode (loops etc.)
- no loops (TCO off)
- no mutable arrays, only immutable trees
- no immutable strings / buffers / textures
- ... what else ... ?