gdnative_core/globalscope.rs
1use std::f32::consts::TAU;
2use std::ops::Rem;
3use std::ops::{Range, RangeInclusive};
4
5const CMP_EPSILON: f32 = 0.00001;
6
7/// Coordinate system conversion: polar -> cartesian
8///
9/// Polar coordinates: distance `r` from the origin + angle `th` (radians).
10/// Cartesian coordinate system: `x` and `y` axis.
11///
12/// Example:
13/// ```
14/// use gdnative::globalscope::*;
15///
16/// let (x, y) = polar2cartesian(13.0, -0.394791119699);
17///
18/// assert_eq!(x, 12.0);
19/// assert_eq!(y, -5.0);
20/// ```
21#[inline]
22pub fn polar2cartesian(r: f32, th: f32) -> (f32, f32) {
23 let x = r * th.cos();
24 let y = r * th.sin();
25
26 (x, y)
27}
28
29/// Coordinate system conversion: cartesian -> polar
30///
31/// Cartesian coordinate system: `x` and `y` axis.
32/// Polar coordinates: distance `r` from the origin + angle `th` (radians).
33///
34/// Example:
35/// ```
36/// use gdnative::globalscope::*;
37///
38/// let (r, th) = cartesian2polar(12.0, -5.0);
39///
40/// assert!(is_equal_approx(r, 13.0));
41/// assert!(is_equal_approx(th, -0.394791119699));
42/// ```
43#[inline]
44pub fn cartesian2polar(x: f32, y: f32) -> (f32, f32) {
45 let r = x.hypot(y);
46 let th = y.atan2(x);
47
48 (r, th)
49}
50
51/// Converts from decibels to linear energy (audio).
52#[inline]
53pub fn db2linear(decibels: f32) -> f32 {
54 f32::exp(decibels * 0.115_129_255)
55}
56
57/// Converts from linear energy to decibels (audio).
58///
59/// This can be used to implement volume sliders that behave as expected (since volume isn't linear).
60#[inline]
61pub fn linear2db(linear_energy: f32) -> f32 {
62 linear_energy.ln() * 0.115_129_255
63}
64
65/// Position of the first non-zero digit, after the decimal point.
66///
67/// Note that the maximum return value is `10`, which is a design decision in the implementation.
68///
69/// # Examples:
70/// ```
71/// use gdnative::globalscope::*;
72///
73/// assert_eq!(step_decimals(5.0), 0);
74/// assert_eq!(step_decimals(12.0004), 4);
75/// assert_eq!(step_decimals(0.000000004), 9);
76/// ```
77#[inline]
78pub fn step_decimals(step: f32) -> i32 {
79 const MAXN: usize = 10;
80 const SD: [f32; MAXN] = [
81 0.9999, // somehow compensate for floating point error
82 0.09999,
83 0.009999,
84 0.0009999,
85 0.00009999,
86 0.000009999,
87 0.0000009999,
88 0.00000009999,
89 0.000000009999,
90 0.0000000009999,
91 ];
92
93 let abs = step.abs();
94 let int_abs: i32 = step as i32;
95 let decs: f32 = abs - (int_abs as f32); // strip away integer part;
96 for (i, item) in SD.iter().enumerate().take(MAXN) {
97 if decs >= *item {
98 return i.try_into().unwrap();
99 }
100 }
101 0
102}
103
104/// Moves `range.start()` toward `range.end()` by the `delta` value.
105///
106/// Use a negative `delta` value `range.end()` to move away.
107/// # Examples:
108/// ```
109/// use gdnative::globalscope::*;
110///
111/// assert_eq!(move_toward(10.0..=5.0, 4.), 6.);
112/// assert_eq!(move_toward(10.0..=5.0, -1.5), 11.5);
113/// assert_eq!(move_toward(4.0..=8.0, 1.0), 5.0);
114/// assert_eq!(move_toward(4.0..=8.0, 5.0), 8.0);
115/// assert_eq!(move_toward(8.0..=4.0, 1.0), 7.0);
116/// assert_eq!(move_toward(8.0..=4.0, 5.0), 4.0);
117/// ```
118#[inline]
119pub fn move_toward(range: RangeInclusive<f32>, delta: f32) -> f32 {
120 if (range.end() - range.start()).abs() <= delta {
121 *range.end()
122 } else {
123 range.start() + (range.end() - range.start()).signum() * delta
124 }
125}
126
127/// Returns an "eased" value of x based on an easing function defined with `curve`.
128///
129/// This easing function is based on an `exponent`. The curve can be any floating-point number,
130/// with specific values leading to the following behaviors:
131///
132/// Value range | Effect
133/// :---: | ---
134/// `s < -1` | Ease in-out
135/// `s == -1` | Linear
136/// `-1 < s < 0` | Ease out-in
137/// `s == 0` | Constant
138/// `0 < s < 1` | Ease out
139/// `s == 1` | Linear
140/// `s > 1` | Ease in
141///
142/// See also [`smoothstep`]. If you need to perform more advanced transitions, use `Tween` or `AnimationPlayer`.
143///
144/// Curve values cheatsheet:
145/// 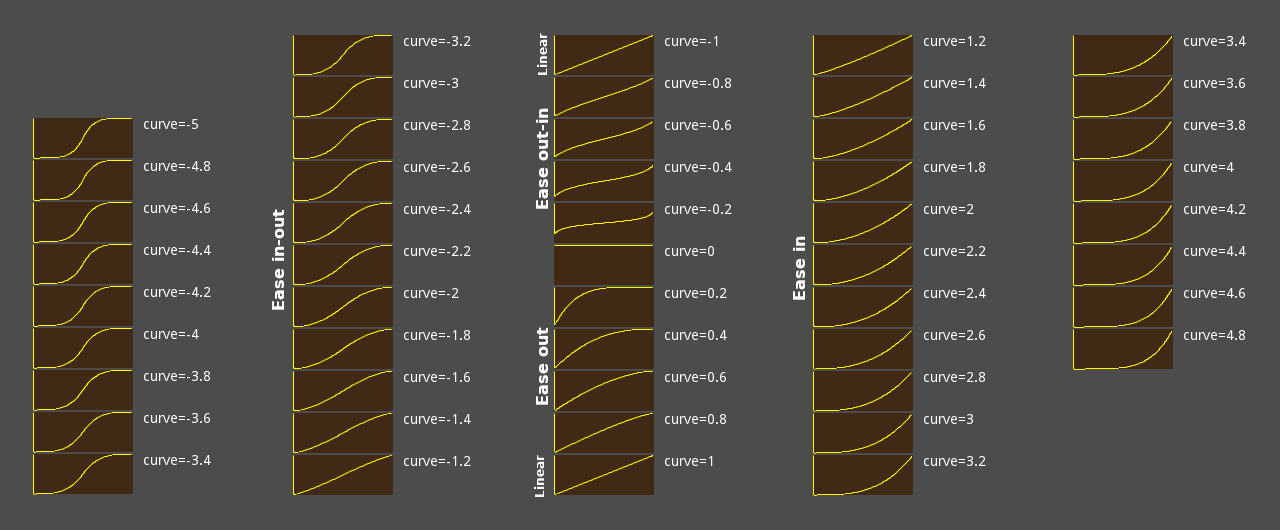
146#[inline]
147pub fn ease(s: f32, curve: f32) -> f32 {
148 let s = s.clamp(0.0, 1.0);
149 if curve > 0.0 {
150 if curve < 1.0 {
151 1.0 - (1.0 - s).powf(1.0 / curve)
152 } else {
153 s.powf(curve)
154 }
155 } else if curve < 0.0 {
156 //inout ease
157
158 if s < 0.5 {
159 (s * 2.0).powf(-curve) * 0.5
160 } else {
161 (1.0 - (1.0 - (s - 0.5) * 2.0).powf(-curve)) * 0.5 + 0.5
162 }
163 } else {
164 0.0 // no ease (raw)
165 }
166}
167
168/// Linearly interpolates between two values, by the factor defined in weight.
169///
170/// To perform interpolation, weight should be between 0.0 and 1.0 (inclusive).
171/// However, values outside this range are allowed and can be used to perform extrapolation.
172/// ```
173/// use gdnative::globalscope::*;
174/// assert_eq!(lerp(0.0..=4.0, 0.75), 3.0);
175/// ```
176#[inline]
177pub fn lerp(range: RangeInclusive<f32>, weight: f32) -> f32 {
178 range.start() + (range.end() - range.start()) * weight
179}
180
181/// Linearly interpolates between two angles (in radians), by a normalized value.
182///
183/// Similar to lerp, but interpolates correctly when the angles wrap around `TAU`.
184/// To perform eased interpolation with `lerp_angle`, combine it with `ease` or `smoothstep`.
185/// ```
186/// use std::f32::consts::{PI, TAU};
187/// use gdnative::globalscope::lerp_angle;
188///
189/// assert_eq!(lerp_angle(-PI..PI, 0.0), -PI);
190/// assert_eq!(lerp_angle(-PI..PI, 1.0), -PI);
191/// assert_eq!(lerp_angle(PI..-PI, 0.0), PI);
192/// assert_eq!(lerp_angle(PI..-PI, 1.0), PI);
193/// assert_eq!(lerp_angle(0.0..TAU, 0.0), 0.0);
194/// assert_eq!(lerp_angle(0.0..TAU, 1.0), 0.0);
195/// assert_eq!(lerp_angle(TAU..0.0, 0.0), TAU);
196/// assert_eq!(lerp_angle(TAU..0.0, 1.0), TAU);
197/// ```
198#[inline]
199pub fn lerp_angle(range: Range<f32>, amount: f32) -> f32 {
200 let difference = f32::rem(range.end - range.start, TAU);
201 let distance = f32::rem(2.0 * difference, TAU) - difference;
202
203 range.start + distance * amount
204}
205
206/// Returns the floating-point modulus of `a/b` that wraps equally in positive and negative.
207///
208/// The result, if not zero, has the same sign as `b`.
209///
210/// # Examples:
211/// ```
212/// use gdnative::globalscope::*;
213///
214/// assert_eq!(fposmod(7.0, 3.0), 1.0);
215/// assert_eq!(fposmod(-7.0, 3.0), 2.0);
216/// assert_eq!(fposmod(7.0, -3.0), -2.0);
217/// assert_eq!(fposmod(-7.0, -3.0), -1.0);
218///
219/// assert_eq!(fposmod(6.0, 3.0), 0.0);
220/// assert_eq!(fposmod(-6.0, 3.0), 0.0);
221/// assert_eq!(fposmod(6.0, -3.0), 0.0);
222/// assert_eq!(fposmod(-6.0, -3.0), 0.0);
223/// ```
224#[inline]
225pub fn fposmod(a: f32, b: f32) -> f32 {
226 let mut value = a % b;
227 if value < 0.0 && b > 0.0 || value > 0.0 && b < 0.0 {
228 value += b;
229 }
230 value
231}
232
233/// Find linear interpolation weight from interpolated values.
234///
235/// Returns an interpolation or extrapolation factor considering the range specified in `range.start()` and `range.end()`,
236/// and the interpolated value specified in `weight`.
237///
238/// The returned value will be between `0.0` and `1.0` if `weight` is between `range.start()` and `range.end()` (inclusive).
239///
240/// If `weight` is located outside this range, then an extrapolation factor will be returned
241/// (return value lower than `0.0` or greater than `1.0`).
242///
243/// # Examples:
244/// ```
245/// use gdnative::globalscope::*;
246///
247/// assert_eq!(inverse_lerp(20.0..=30.0, 27.5), 0.75);
248/// ```
249#[inline]
250pub fn inverse_lerp(range: RangeInclusive<f32>, value: f32) -> f32 {
251 (value - range.start()) / (range.end() - range.start())
252}
253
254/// Smooth (Hermite) interpolation.
255///
256/// Returns the result of smoothly interpolating the value of `s` between `0` and `1`, based on where `s` lies
257/// with respect to the edges `from` and `to`.
258///
259/// The return value is `0` if `s <= from`, and `1` if `s >= to`.
260///
261/// If `s` lies between `from` and `to`, the returned value follows an S-shaped curve that maps `s` between `0` and `1`.
262/// This S-shaped curve is the cubic Hermite interpolator, given by `f(y) = 3*y^2 - 2*y^3` where `y = (x-from) / (to-from)`.
263///
264/// Compared to [`ease()`] with a curve value of `-1.6521`, `smoothstep()` returns the smoothest possible curve with no
265/// sudden changes in the derivative.
266///
267/// If you need to perform more advanced transitions, use `Tween` or `AnimationPlayer`.
268/// # Examples:
269/// ```
270/// use gdnative::globalscope::*;
271///
272/// assert_eq!(smoothstep(0.0, 2.0, -5.0), 0.0);
273/// assert_eq!(smoothstep(0.0, 2.0, 0.5), 0.15625);
274/// assert_eq!(smoothstep(0.0, 2.0, 1.0), 0.5);
275/// assert_eq!(smoothstep(0.0, 2.0, 2.0), 1.0);
276/// ```
277#[inline]
278pub fn smoothstep(from: f32, to: f32, s: f32) -> f32 {
279 if is_equal_approx(from, to) {
280 return from;
281 }
282 let s = ((s - from) / (to - from)).clamp(0.0, 1.0);
283 s * s * (3.0 - 2.0 * s)
284}
285
286/// Returns `true` if `a` and `b` are approximately equal to each other.
287///
288/// Here, approximately equal means that `a` and `b` are within a small internal epsilon of each other,
289/// which scales with the magnitude of the numbers.
290///
291/// Infinity values of the same sign are considered equal.
292#[inline]
293pub fn is_equal_approx(a: f32, b: f32) -> bool {
294 if a == b {
295 return true;
296 }
297 let mut tolerance = CMP_EPSILON * a.abs();
298 if tolerance < CMP_EPSILON {
299 tolerance = CMP_EPSILON;
300 }
301 (a - b).abs() < tolerance
302}
303
304/// Returns true if `s` is zero or almost zero.
305///
306/// This method is faster than using is_equal_approx with one value as zero.
307#[inline]
308pub fn is_zero_approx(s: f32) -> bool {
309 s.abs() < CMP_EPSILON
310}
311
312/// Returns the nearest equal or larger power of 2 for an integer value.
313///
314/// In other words, returns the smallest value a where `a = pow(2, n)` such that `value <= a` for some non-negative integer `n`.
315///
316/// This behaves like [`u32::next_power_of_two()`] for `value >= 1`.
317///
318/// **Warning:** This function returns 0 rather than 1 for non-positive values of `value`
319/// (in reality, 1 is the smallest integer power of 2).
320///
321/// # Examples:
322/// ```
323/// use gdnative::globalscope::*;
324///
325/// assert_eq!(nearest_po2(3), 4);
326/// assert_eq!(nearest_po2(4), 4);
327/// assert_eq!(nearest_po2(5), 8);
328/// assert_eq!(nearest_po2(0), 0);
329/// assert_eq!(nearest_po2(-1), 0);
330/// ```
331#[inline]
332pub fn nearest_po2(value: i32) -> u32 {
333 if value <= 0 {
334 return 0;
335 }
336 (value as u32).next_power_of_two()
337}
338
339/// Returns the integer modulus of `a/b` that wraps equally in positive and negative.
340///
341/// The result, if not zero, has the same sign as `b`.
342///
343/// # Examples:
344/// ```
345/// use gdnative::globalscope::*;
346///
347/// assert_eq!(posmod(7, 3), 1);
348/// assert_eq!(posmod(-7, 3), 2);
349/// assert_eq!(posmod(7, -3), -2);
350/// assert_eq!(posmod(-7, -3), -1);
351///
352/// assert_eq!(posmod(6, 3), 0);
353/// assert_eq!(posmod(-6, 3), 0);
354/// assert_eq!(posmod(6, -3), 0);
355/// assert_eq!(posmod(-6, -3), 0);
356/// ```
357#[inline]
358pub fn posmod(a: i32, b: i32) -> i32 {
359 let mut value = a % b;
360 if value < 0 && b > 0 || value > 0 && b < 0 {
361 value += b;
362 }
363 value
364}
365
366/// Maps a value from `range_from` to `range_to`, using linear interpolation.
367///
368/// # Example:
369/// ```
370/// use gdnative::globalscope::*;
371///
372/// assert_eq!(range_lerp(75.0, 0.0..=100.0, -1.0..=1.0), 0.5);
373/// ```
374#[inline]
375pub fn range_lerp(
376 value: f32,
377 range_from: RangeInclusive<f32>,
378 range_to: RangeInclusive<f32>,
379) -> f32 {
380 lerp(range_to, inverse_lerp(range_from, value))
381}
382
383/// Snaps float value `s` to a given `step`.
384///
385/// This can also be used to round a floating point number to an arbitrary number of decimals.
386/// ```
387/// use gdnative::globalscope::*;
388/// use std::f32::consts::E; // Euler constant, 2.71828
389///
390/// assert_eq!(stepify(100.0, 32.0), 96.0);
391/// assert_eq!(stepify(E, 0.01), 2.72);
392/// ```
393#[inline]
394pub fn stepify(mut value: f32, step: f32) -> f32 {
395 if step != 0.0 {
396 value = (value / step + 0.5).floor() * step;
397 }
398 value
399}
400
401/// Wraps float value between `min` and `max`.
402///
403/// Usable for creating loop-alike behavior or infinite surfaces.
404///
405/// # Examples:
406/// ```
407/// use gdnative::globalscope::*;
408/// use std::f32::consts::{TAU, PI};
409///
410/// // Custom range
411/// assert_eq!(wrapf(3.2, 0.5..2.5), 1.2);
412///
413/// // Full circle
414/// let angle = 3.0 * PI;
415/// assert!(is_equal_approx(wrapf(angle, 0.0..TAU), PI));
416/// ```
417///
418/// If the range start is 0, this is equivalent to [`fposmod()`], so prefer using that instead.
419///
420/// Note that unlike GDScript's method, the range must be non-empty and non-inverted.
421///
422/// # Panics
423/// If the range is empty, i.e. `range.start` >= `range.end`.
424#[inline]
425pub fn wrapf(value: f32, range: Range<f32>) -> f32 {
426 assert!(
427 !range.is_empty(),
428 "wrapf expects non-empty, non-inverted range; passed {}..{}",
429 range.start,
430 range.end
431 );
432
433 let range_diff = range.end - range.start;
434 value - range_diff * ((value - range.start) / range_diff).floor()
435}
436
437/// Wraps integer value between `min` and `max`.
438///
439/// Usable for creating loop-alike behavior or infinite surfaces.
440///
441/// # Examples:
442/// ```
443/// use gdnative::globalscope::*;
444///
445/// assert_eq!(wrapi(5, 3..5), 3);
446/// assert_eq!(wrapi(1, -1..2), 1);
447/// assert_eq!(wrapi(-1, 2..4), 3);
448/// ```
449///
450/// If the range start is 0, this is equivalent to [`posmod()`], so prefer using that instead.
451///
452/// Note that unlike GDScript's method, the range must be non-empty and non-inverted.
453///
454/// # Panics
455/// If the range is empty, i.e. `range.start` >= `range.end`.
456#[inline]
457pub fn wrapi(value: i32, range: Range<i32>) -> i32 {
458 assert!(
459 !range.is_empty(),
460 "wrapf expects non-empty, non-inverted range; passed {}..{}",
461 range.start,
462 range.end
463 );
464
465 let range_diff = range.end - range.start;
466 range.start + (value - range.start % range_diff + range_diff) % range_diff
467}