Enum Digit 

#[repr(u8)]
pub enum Digit {
    Neg = 0,
    Zero = 1,
    Pos = 2,
}

Module: Balanced Ternary Digit

This module defines the Digit type for the balanced ternary numeral system, along with its associated operations and functionality.

Represents a digit in the balanced ternary numeral system.

A digit can have one of three values:

• Neg (-1): Represents the value -1 in the balanced ternary system.
• Zero (0): Represents the value 0 in the balanced ternary system.
• Pos (+1): Represents the value +1 in the balanced ternary system.

Provides utility functions for converting to/from characters, integers, and negation.

Key Features

• Digit Type: Represents a digit in the balanced ternary numeral system.
  • Possible values: Neg (-1), Zero (0), Pos (+1).
  • Provides utility functions for converting between characters, integers, and other formats.
• Arithmetic Operators: Implements arithmetic operations for digits, including:
  • Negation (Neg) and Bitwise Not (Not).
  • Addition (Add) and Subtraction (Sub).
  • Multiplication (Mul) and Division (Div), with safe handling of divisors (division by zero panics).
• Logical Operators: Supports bitwise logical operations (AND, OR, XOR) based on ternary logic rules.
• Custom Methods: Additional utility methods implementing balanced ternary logic principles.

Supported Use Cases

• Arithmetic in balanced ternary numeral systems.
• Logic operations in custom numeral systems.
• Conversion between balanced ternary representation and more common formats like integers and characters.

Digit type arithmetical and logical operations

• Neg and Not for Digit: Negates the digit value, adhering to balanced ternary rules.
• Add<Digit> for Digit: Adds two Digit values and returns a Digit.
• Sub<Digit> for Digit: Subtracts one Digit from another and returns a Digit.
• Mul<Digit> for Digit: Multiplies two Digit values and returns a Digit.
• Div<Digit> for Digit: Divides one Digit by another and returns a Digit. Division by zero panics.

Logical Operations for Digit

The Digit type supports bitwise logical operations, which are implemented according to logical rules applicable to balanced ternary digits.

Digits operations

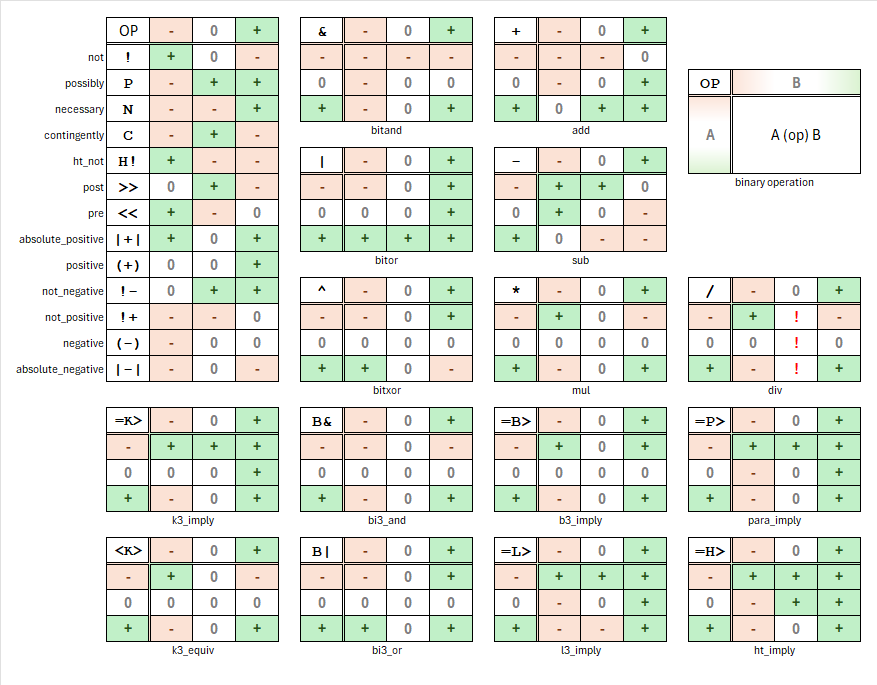
/, *, &, | and ^ should not be used with Ternary::each_{with,zip}(). Instead, use these operators from Ternary directly.

Do so to add and sub ternaries, too.

Variants

Neg = 0

Represents -1

Zero = 1

Represents 0

Pos = 2

Represents +1

Implementations

impl Digit

pub const fn to_char_theta(&self) -> char

Converts the Digit into a character representation.

• Returns:
  • Θ for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos

pub const fn to_char_z(&self) -> char

Converts the Digit into a character representation.

• Returns:
  • Z for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos

pub const fn to_char_t(&self) -> char

Converts the Digit into a character representation.

• Returns:
  • T for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos

pub const fn from_char_theta(c: char) -> Digit

Creates a Digit from a character representation.

• Accepts:
  • Θ for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos
• Panics if the input character is invalid.

pub const fn from_char_z(c: char) -> Digit

Creates a Digit from a character representation.

• Accepts:
  • Z for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos
• Panics if the input character is invalid.

pub const fn from_char_t(c: char) -> Digit

Creates a Digit from a character representation.

• Accepts:
  • T for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos
• Panics if the input character is invalid.

pub const fn to_char(&self) -> char

Converts the Digit into its character representation.

• Returns:
  • - for Digit::Neg
  • 0 for Digit::Zero
  • + for Digit::Pos

pub const fn from_char(c: char) -> Digit

Creates a Digit from its character representation.

• Accepts:
  • - for Digit::Neg
  • 0 for Digit::Zero
  • + for Digit::Pos
• Panics if the input character is invalid.

pub const fn to_i8(&self) -> i8

Converts the Digit into its integer representation.

• Returns:
  • -1 for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos

pub const fn from_i8(i: i8) -> Digit

Creates a Digit from its integer representation.

• Accepts:
  • -1 for Digit::Neg
  • 0 for Digit::Zero
  • 1 for Digit::Pos
• Panics if the input integer is invalid.

pub const fn possibly(self) -> Self

Returns the corresponding possible value of the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Pos for Digit::Zero
  • Digit::Pos for Digit::Pos

pub const fn necessary(self) -> Self

Determines the condition of necessity for the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Neg for Digit::Zero
  • Digit::Pos for Digit::Pos

This method is used to calculate necessity as part of balanced ternary logic systems.

pub const fn contingently(self) -> Self

Determines the condition of contingency for the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Pos for Digit::Zero
  • Digit::Neg for Digit::Pos

This method represents contingency in balanced ternary logic, which defines the specific alternation of Digit values.

pub const fn absolute_positive(self) -> Self

Returns the absolute positive value of the current Digit.

• Returns:
  • Digit::Pos for Digit::Neg
  • Digit::Zero for Digit::Zero
  • Digit::Pos for Digit::Pos

pub const fn positive(self) -> Self

Determines the strictly positive condition for the current Digit.

• Returns:
  • Digit::Zero for Digit::Neg
  • Digit::Zero for Digit::Zero
  • Digit::Pos for Digit::Pos

This method is used to calculate strictly positive states in association with ternary logic.

pub const fn not_negative(self) -> Self

Determines the condition of non-negativity for the current Digit.

• Returns:
  • Digit::Zero for Digit::Neg
  • Digit::Pos for Digit::Zero
  • Digit::Pos for Digit::Pos

This method is used to filter out negative conditions in computations with balanced ternary representations.

pub const fn not_positive(self) -> Self

Determines the condition of non-positivity for the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Neg for Digit::Zero
  • Digit::Zero for Digit::Pos

This method complements the positive condition and captures states that are not strictly positive.

pub const fn negative(self) -> Self

Determines the strictly negative condition for the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Zero for Digit::Zero
  • Digit::Zero for Digit::Pos

This method calculates strictly negative states in association with ternary logic.

pub const fn absolute_negative(self) -> Self

Returns the absolute negative value of the current Digit.

• Returns:
  • Digit::Neg for Digit::Neg
  • Digit::Zero for Digit::Zero
  • Digit::Neg for Digit::Pos

pub const fn k3_imply(self, other: Self) -> Self

Performs Kleene implication with the current Digit as self and another Digit.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Pos when self is Digit::Neg.
  • The positive condition of other when self is Digit::Zero.
  • other when self is Digit::Pos.

Implements Kleene ternary implication logic, which includes determining the logical result based on antecedent and consequent.

pub const fn k3_equiv(self, other: Self) -> Self

Apply a ternary equivalence operation for the current Digit and another Digit.

• self: The first operand of the equivalence operation.

• other: The second operand of the equivalence operation.

• Returns:

  • The negation of other when self is Digit::Neg.
  • Digit::Zero when self is Digit::Zero.
  • other when self is Digit::Pos.

This method implements a ternary logic equivalence, which captures the relationship between two balanced ternary Digits based on their logical equivalence.

pub const fn bi3_and(self, other: Self) -> Self

Performs a ternary AND operation for the current Digit and another Digit.

• self: The first operand of the AND operation.

• other: The second operand of the AND operation.

• Returns:

  • Digit::Neg if self is Digit::Neg and other is not Digit::Zero.
  • Digit::Zero if either self or other is Digit::Zero.
  • other if self is Digit::Pos.

This method implements Bochvar’s internal three-valued logic in balanced ternary AND operation, which evaluates the logical conjunction of two Digits in the ternary logic system.

pub const fn bi3_or(self, other: Self) -> Self

Performs a ternary OR operation for the current Digit and another Digit.

• self: The first operand of the OR operation.

• other: The second operand of the OR operation.

• Returns:

  • other if self is Digit::Neg.
  • Digit::Zero if self is Digit::Zero.
  • Digit::Pos if self is Digit::Pos and other is not Digit::Zero.

This method implements Bochvar’s three-valued internal ternary logic for the OR operation, determining the logical disjunction of two balanced ternary Digits.

pub const fn bi3_imply(self, other: Self) -> Self

Performs Bochvar’s internal three-valued implication with the current Digit as self and another Digit as the consequent.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Zero if self is Digit::Neg and other is Digit::Zero.
  • Digit::Pos if self is Digit::Neg and other is not Digit::Zero.
  • Digit::Zero if self is Digit::Zero.
  • other if self is Digit::Pos.

This method implements Bochvar’s internal implication logic, which evaluates the logical consequence, between two balanced ternary Digits in a manner consistent with three-valued logic principles.

pub const fn l3_imply(self, other: Self) -> Self

Performs Łukasiewicz implication with the current Digit as self and another Digit.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Pos when self is Digit::Neg.
  • The non-negative condition of other when self is Digit::Zero.
  • other when self is Digit::Pos.

Implements Łukasiewicz ternary implication logic, which evaluates an alternative approach for implication compared to Kleene logic.

pub const fn rm3_imply(self, other: Self) -> Self

Performs RM3 implication with the current Digit as self and another Digit.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Pos when self is Digit::Neg.
  • other when self is Digit::Zero.
  • The necessary condition of other when self is Digit::Pos.

Implements RM3 ternary implication logic, which defines a unique perspective for implication operations in balanced ternary systems.

pub const fn para_imply(self, other: Self) -> Self

Performs the paraconsistent-logic implication with the current Digit as self and another Digit.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Pos when self is Digit::Neg.
  • other otherwise.

pub const fn ht_imply(self, other: Self) -> Self

Performs HT implication with the current Digit as self and another Digit.

• self: The antecedent of the implication.

• other: The consequent of the implication.

• Returns:

  • Digit::Pos when self is Digit::Neg.
  • The possibility condition of other when self is Digit::Zero.
  • other when self is Digit::Pos.

This method computes HT ternary implication based on heuristic logic.

pub const fn ht_not(self) -> Self

Performs HT logical negation of the current Digit.

• Returns:
  • Digit::Pos when self is Digit::Neg.
  • Digit::Neg when self is Digit::Zero or Digit::Pos.

This method evaluates the HT negation result using heuristic ternary logic.

pub const fn ht_bool(self) -> bool

Converts the Digit to a bool in HT logic.

• Returns:

  • true when self is Digit::Pos.
  • false when self is Digit::Neg.

• Panics:

  • Panics if self is Digit::Zero, as Digit::Zero cannot be directly converted to a boolean value.

    To ensure Pos or Neg value, use one of :

    • Digit::possibly
    • Digit::necessary
    • Digit::contingently
    • Digit::ht_not

pub const fn post(self) -> Self

Performs Post’s negation of the current Digit.

• Returns:
  • Digit::Zero when self is Digit::Neg.
  • Digit::Pos when self is Digit::Zero.
  • Digit::Neg when self is Digit::Pos.

This method evaluates the negation based on Post’s logic in ternary systems, which differs from standard negation logic.

pub const fn pre(self) -> Self

Performs the inverse operation from the Post’s negation of the current Digit.

• Returns:
  • Digit::Pos when self is Digit::Neg.
  • Digit::Neg when self is Digit::Zero.
  • Digit::Zero when self is Digit::Pos.

pub const fn to_unbalanced(self) -> u8

This method maps this Digit value to its corresponding unbalanced ternary integer representation.

• Returns:
  • 0 for Digit::Neg.
  • 1 for Digit::Zero.
  • 2 for Digit::Pos.

pub const fn from_unbalanced(u: u8) -> Digit

Creates a Digit from an unbalanced ternary integer representation.

Arguments:

• u: An unsigned 8-bit integer representing an unbalanced ternary value.

Returns:

• Digit::Neg for 0.
• Digit::Zero for 1.
• Digit::Pos for 2.

Panics:

• Panics if the provided value is not 0, 1, or 2, as these are the only valid representations of unbalanced ternary values.

pub fn inc(self) -> Ternary

Increments the Digit value and returns a Ternary result.

• The rules for incrementing are based on ternary arithmetic:

  • For Digit::Neg:
    • Incrementing results in Digit::Zero (Ternary::parse("0")).
  • For Digit::Zero:
    • Incrementing results in Digit::Pos (Ternary::parse("+")).
  • For Digit::Pos:
    • Incrementing results in “overflow” (Ternary::parse("+-")).

• Returns:

  • A Ternary instance representing the result of the increment operation.

pub fn dec(self) -> Ternary

Decrements the Digit value and returns a Ternary result.

• The rules for decrementing are based on ternary arithmetic:

  • For Digit::Neg:
    • Decrementing results in “underflow” (Ternary::parse("-+")).
  • For Digit::Zero:
    • Decrementing results in Digit::Neg (Ternary::parse("-")).
  • For Digit::Pos:
    • Decrementing results in Digit::Zero (Ternary::parse("0")).

• Returns:

  • A Ternary instance representing the result of the decrement operation.

Trait Implementations

impl Add<Digit> for &Ternary

type Output = Ternary

The resulting type after applying the + operator.

fn add(self, rhs: Digit) -> Self::Output

Performs the + operation.

impl Add for Digit

fn add(self, other: Digit) -> Self::Output

Adds two Digit values together and returns a Digit result.

• Returns:

  • A Ternary instance that holds the result of the addition.

• Panics:

  • This method does not panic under any circumstances.

type Output = Digit

The resulting type after applying the + operator.

impl BitAnd for Digit

fn bitand(self, other: Self) -> Self::Output

Performs a bitwise AND operation between two Digit values and returns the result.

• The rules for the bitwise AND (&) operation are:
  • If self is Digit::Neg, the result is always Digit::Neg.
  • If self is Digit::Zero, the result depends on the value of other:
    • Digit::Neg results in Digit::Neg.
    • Otherwise, the result is Digit::Zero.
  • If self is Digit::Pos, the result is simply other.

Returns:

• A Digit value that is the result of the bitwise AND operation.

Examples:

use balanced_ternary::Digit;
use Digit::{Neg, Pos, Zero};

assert_eq!(Neg & Pos, Neg);
assert_eq!(Zero & Neg, Neg);
assert_eq!(Zero & Pos, Zero);
assert_eq!(Pos & Zero, Zero);

type Output = Digit

The resulting type after applying the & operator.

impl BitOr for Digit

fn bitor(self, other: Self) -> Self::Output

Performs a bitwise OR operation between two Digit values and returns the result.

• The rules for the bitwise OR (|) operation are as follows:
  • If self is Digit::Neg, the result is always the value of other.
  • If self is Digit::Zero, the result depends on the value of other:
    • Digit::Pos results in Digit::Pos.
    • Otherwise, the result is Digit::Zero.
  • If self is Digit::Pos, the result is always Digit::Pos.

Returns:

• A Digit value that is the result of the bitwise OR operation.

Examples:

use balanced_ternary::Digit;
use Digit::{Neg, Pos, Zero};

assert_eq!(Neg | Pos, Pos);
assert_eq!(Zero | Neg, Zero);
assert_eq!(Zero | Pos, Pos);
assert_eq!(Pos | Zero, Pos);

type Output = Digit

The resulting type after applying the | operator.

impl BitXor for Digit

fn bitxor(self, rhs: Self) -> Self::Output

Performs a bitwise XOR (exclusive OR) operation between two Digit values.

• The rules for the bitwise XOR (^) operation are as follows:
  • If self is Digit::Neg, the result is always the value of rhs.
  • If self is Digit::Zero, the result is always Digit::Zero.
  • If self is Digit::Pos, the result is the negation of rhs:
    • Digit::Neg becomes Digit::Pos.
    • Digit::Zero becomes Digit::Zero.
    • Digit::Pos becomes Digit::Neg.

Returns:

• A Digit value that is the result of the bitwise XOR operation.

Examples:

use balanced_ternary::Digit;
use Digit::{Neg, Pos, Zero};

assert_eq!(Neg ^ Pos, Pos);
assert_eq!(Zero ^ Neg, Zero);
assert_eq!(Pos ^ Pos, Neg);

type Output = Digit

The resulting type after applying the ^ operator.

impl Clone for Digit

fn clone(&self) -> Digit

Returns a duplicate of the value.

fn clone_from(&mut self, source: &Self)

Performs copy-assignment from source.

impl Debug for Digit

fn fmt(&self, f: &mut Formatter<'_>) -> Result

Formats the value using the given formatter.

impl Div for Digit

fn div(self, other: Digit) -> Self::Output

Divides one Digit value by another and returns the result as a Digit.

Rules for division:

• For Digit::Neg:
  • Dividing Digit::Neg by Digit::Neg results in Digit::Pos.
  • Dividing Digit::Neg by Digit::Zero will panic with “Cannot divide by zero.”
  • Dividing Digit::Neg by Digit::Pos results in Digit::Neg.
• For Digit::Zero:
  • Dividing Digit::Zero by Digit::Neg results in Digit::Zero.
  • Dividing Digit::Zero by Digit::Zero will panic with “Cannot divide by zero.”
  • Dividing Digit::Zero by Digit::Pos results in Digit::Zero.
• For Digit::Pos:
  • Dividing Digit::Pos by Digit::Neg results in Digit::Neg.
  • Dividing Digit::Pos by Digit::Zero will panic with “Cannot divide by zero.”
  • Dividing Digit::Pos by Digit::Pos results in Digit::Pos.

Returns:

• A Digit value representing the result of the division.

Panics:

• Panics with “Cannot divide by zero.” if the other operand is Digit::Zero.

type Output = Digit

The resulting type after applying the / operator.

impl From<Digit> for char

fn from(value: Digit) -> Self

Converts to this type from the input type.

impl From<Digit> for i8

fn from(value: Digit) -> Self

Converts to this type from the input type.

impl From<char> for Digit

fn from(value: char) -> Self

Converts to this type from the input type.

impl From<i8> for Digit

fn from(value: i8) -> Self

Converts to this type from the input type.

impl Hash for Digit

fn hash<__H: Hasher>(&self, state: &mut __H)

Feeds this value into the given Hasher.

fn hash_slice<H>(data: &[Self], state: &mut H)

where H: Hasher, Self: Sized,

Feeds a slice of this type into the given Hasher.

impl Mul for Digit

fn mul(self, other: Digit) -> Self::Output

Multiplies two Digit values together and returns the product as a Digit.

• The rules for multiplication in this implementation are straightforward:

  • Digit::Neg multiplied by:
    • Digit::Neg results in Digit::Pos.
    • Digit::Zero results in Digit::Zero.
    • Digit::Pos results in Digit::Neg.
  • Digit::Zero multiplied by any Digit always results in Digit::Zero.
  • Digit::Pos multiplied by:
    • Digit::Neg results in Digit::Neg.
    • Digit::Zero results in Digit::Zero.
    • Digit::Pos results in Digit::Pos.

• Returns:

  • A Digit instance representing the result of the multiplication.

type Output = Digit

The resulting type after applying the * operator.

impl Neg for Digit

fn neg(self) -> Self::Output

Returns the negation of the Digit.

• Digit::Neg becomes Digit::Pos
• Digit::Pos becomes Digit::Neg
• Digit::Zero remains Digit::Zero

type Output = Digit

The resulting type after applying the - operator.

impl Not for Digit

type Output = Digit

The resulting type after applying the ! operator.

fn not(self) -> Self::Output

Performs the unary ! operation.

impl PartialEq for Digit

fn eq(&self, other: &Digit) -> bool

Tests for self and other values to be equal, and is used by ==.

fn ne(&self, other: &Rhs) -> bool

Tests for !=. The default implementation is almost always sufficient, and should not be overridden without very good reason.

impl Sub<Digit> for &Ternary

type Output = Ternary

The resulting type after applying the - operator.

fn sub(self, rhs: Digit) -> Self::Output

Performs the - operation.

impl Sub for Digit

fn sub(self, other: Digit) -> Self::Output

Subtracts two Digit values and returns a Digit result.

• Returns:

  • A Ternary instance that holds the result of the subtraction.

• Panics:

  • This method does not panic under any circumstances.

type Output = Digit

The resulting type after applying the - operator.

impl Copy for Digit

impl Eq for Digit

impl StructuralPartialEq for Digit