Function solve_pnp_generic 

pub fn solve_pnp_generic(
    object_points: &impl ToInputArray,
    image_points: &impl ToInputArray,
    camera_matrix: &impl ToInputArray,
    dist_coeffs: &impl ToInputArray,
    rvecs: &mut impl ToOutputArray,
    tvecs: &mut impl ToOutputArray,
    use_extrinsic_guess: bool,
    flags: SolvePnPMethod,
    rvec: &impl ToInputArray,
    tvec: &impl ToInputArray,
    reprojection_error: &mut impl ToOutputArray,
) -> Result<i32>

Finds an object pose from 3D-2D point correspondences.

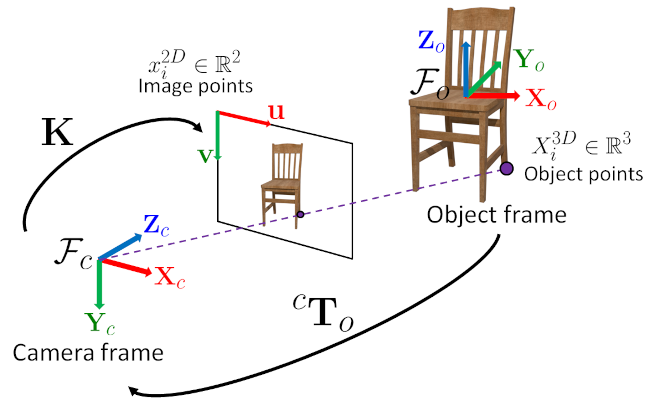{ width=50% }

See also

[calib3d_solvePnP]

This function returns a list of all the possible solutions (a solution is a <rotation vector, translation vector> couple), depending on the number of input points and the chosen method:

• P3P methods (SOLVEPNP_P3P, SOLVEPNP_AP3P): 3 or 4 input points. Number of returned solutions can be between 0 and 4 with 3 input points.
• SOLVEPNP_IPPE Input points must be >= 4 and object points must be coplanar. Returns 2 solutions.
• SOLVEPNP_IPPE_SQUARE Special case suitable for marker pose estimation. Number of input points must be 4 and 2 solutions are returned. Object points must be defined in the following order:
  • point 0: [-squareLength / 2, squareLength / 2, 0]
  • point 1: [ squareLength / 2, squareLength / 2, 0]
  • point 2: [ squareLength / 2, -squareLength / 2, 0]
  • point 3: [-squareLength / 2, -squareLength / 2, 0]
• for all the other flags, number of input points must be >= 4 and object points can be in any configuration. Only 1 solution is returned.

Parameters

• objectPoints: Array of object points in the object coordinate space, Nx3 1-channel or 1xN/Nx1 3-channel, where N is the number of points. vector<Point3d> can be also passed here.
• imagePoints: Array of corresponding image points, Nx2 1-channel or 1xN/Nx1 2-channel, where N is the number of points. vector<Point2d> can be also passed here.
• cameraMatrix: Input camera intrinsic matrix .
• distCoeffs: Input vector of distortion coefficients . If the vector is NULL/empty, the zero distortion coefficients are assumed.
• rvecs: Vector of output rotation vectors (see [Rodrigues] ) that, together with tvecs, brings points from the model coordinate system to the camera coordinate system.
• tvecs: Vector of output translation vectors.
• useExtrinsicGuess: Parameter used for #SOLVEPNP_ITERATIVE. If true (1), the function uses the provided rvec and tvec values as initial approximations of the rotation and translation vectors, respectively, and further optimizes them.
• flags: Method for solving a PnP problem: see [calib3d_solvePnP_flags]
• rvec: Rotation vector used to initialize an iterative PnP refinement algorithm, when flag is SOLVEPNP_ITERATIVE and useExtrinsicGuess is set to true.
• tvec: Translation vector used to initialize an iterative PnP refinement algorithm, when flag is SOLVEPNP_ITERATIVE and useExtrinsicGuess is set to true.
• reprojectionError: Optional vector of reprojection error, that is the RMS error () between the input image points and the 3D object points projected with the estimated pose.

More information is described in [calib3d_solvePnP]

Note:

• An example of how to use solvePnP for planar augmented reality can be found at opencv_source_code/samples/python/plane_ar.py
• If you are using Python:
  • Numpy array slices won’t work as input because solvePnP requires contiguous arrays (enforced by the assertion using cv::Mat::checkVector() around line 55 of modules/calib3d/src/solvepnp.cpp version 2.4.9)
  • The P3P algorithm requires image points to be in an array of shape (N,1,2) due to its calling of undistort_points (around line 75 of modules/calib3d/src/solvepnp.cpp version 2.4.9) which requires 2-channel information.
  • Thus, given some data D = np.array(…) where D.shape = (N,M), in order to use a subset of it as, e.g., imagePoints, one must effectively copy it into a new array: imagePoints = np.ascontiguousarray(D[:,:2]).reshape((N,1,2))
• The methods SOLVEPNP_DLS and SOLVEPNP_UPNP cannot be used as the current implementations are unstable and sometimes give completely wrong results. If you pass one of these two flags, SOLVEPNP_EPNP method will be used instead.
• The minimum number of points is 4 in the general case. In the case of SOLVEPNP_P3P and SOLVEPNP_AP3P methods, it is required to use exactly 4 points (the first 3 points are used to estimate all the solutions of the P3P problem, the last one is used to retain the best solution that minimizes the reprojection error).
• With SOLVEPNP_ITERATIVE method and useExtrinsicGuess=true, the minimum number of points is 3 (3 points are sufficient to compute a pose but there are up to 4 solutions). The initial solution should be close to the global solution to converge.
• With SOLVEPNP_IPPE input points must be >= 4 and object points must be coplanar.
• With SOLVEPNP_IPPE_SQUARE this is a special case suitable for marker pose estimation. Number of input points must be 4. Object points must be defined in the following order:
  • point 0: [-squareLength / 2, squareLength / 2, 0]
  • point 1: [ squareLength / 2, squareLength / 2, 0]
  • point 2: [ squareLength / 2, -squareLength / 2, 0]
  • point 3: [-squareLength / 2, -squareLength / 2, 0]
• With SOLVEPNP_SQPNP input points must be >= 3

C++ default parameters

• use_extrinsic_guess: false
• flags: SOLVEPNP_ITERATIVE
• rvec: noArray()
• tvec: noArray()
• reprojection_error: noArray()