[−][src]Struct fst::raw::Fst
An acyclic deterministic finite state transducer.
How does it work?
The short answer: it's just like a prefix trie, which compresses keys based only on their prefixes, except that a automaton/transducer also compresses suffixes.
The longer answer is that keys in an automaton are stored only in the transitions from one state to another. A key can be acquired by tracing a path from the root of the automaton to any match state. The inputs along each transition are concatenated. Once a match state is reached, the concatenation of inputs up until that point corresponds to a single key.
But why is it called a transducer instead of an automaton? A finite state transducer is just like a finite state automaton, except that it has output transitions in addition to input transitions. Namely, the value associated with any particular key is determined by summing the outputs along every input transition that leads to the key's corresponding match state.
This is best demonstrated with a couple images. First, let's ignore the "transducer" aspect and focus on a plain automaton.
Consider that your keys are abbreviations of some of the months in the Gregorian calendar:
jan
feb
mar
apr
may
jun
jul
The corresponding automaton that stores all of these as keys looks like this:
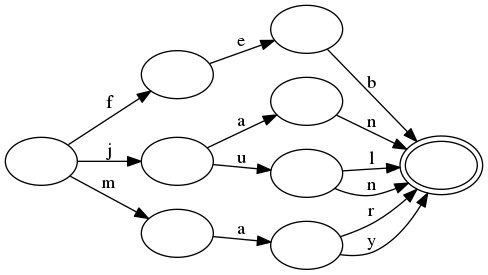
Notice here how the prefix and suffix of jan and jun are shared.
Similarly, the prefixes of jun and jul are shared and the prefixes
of mar and may are shared.
All of the keys from this automaton can be enumerated in lexicographic order by following every transition from each node in lexicographic order. Since it is acyclic, the procedure will terminate.
A key can be found by tracing it through the transitions in the automaton.
For example, the key aug is known not to be in the automaton by only
visiting the root state (because there is no a transition). For another
example, the key jax is known not to be in the set only after moving
through the transitions for j and a. Namely, after those transitions
are followed, there are no transitions for x.
Notice here that looking up a key is proportional the length of the key itself. Namely, lookup time is not affected by the number of keys in the automaton!
Additionally, notice that the automaton exploits the fact that many keys
share common prefixes and suffixes. For example, jun and jul are
represented with no more states than would be required to represent either
one on its own. Instead, the only change is a single extra transition. This
is a form of compression and is key to how the automatons produced by this
crate are so small.
Let's move on to finite state transducers. Consider the same set of keys as above, but let's assign their numeric month values:
jan,1
feb,2
mar,3
apr,4
may,5
jun,6
jul,7
The corresponding transducer looks very similar to the automaton above, except outputs have been added to some of the transitions:
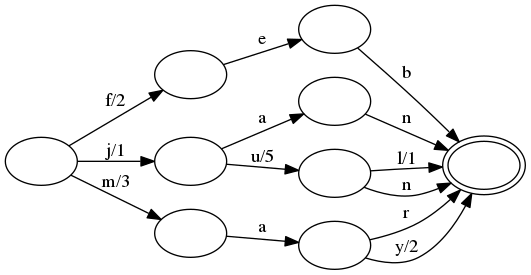
All of the operations with a transducer are the same as described above for automatons. Additionally, the same compression techniques are used: common prefixes and suffixes in keys are exploited.
The key difference is that some transitions have been given an output.
As one follows input transitions, one must sum the outputs as they
are seen. (A transition with no output represents the additive identity,
or 0 in this case.) For example, when looking up feb, the transition
f has output 2, the transition e has output 0, and the transition
b also has output 0. The sum of these is 2, which is exactly the
value we associated with feb.
For another more interesting example, consider jul. The j transition
has output 1, the u transition has output 5 and the l transition
has output 1. Summing these together gets us 7, which is again the
correct value associated with jul. Notice that if we instead looked up
the jun key, then the n transition would be followed instead of the
l transition, which has no output. Therefore, the jun key equals
1+5+0=6.
The trick to transducers is that there exists a unique path through the transducer for every key, and its outputs are stored appropriately along this path such that the correct value is returned when they are all summed together. This process also enables the data that makes up each value to be shared across many values in the transducer in exactly the same way that keys are shared. This is yet another form of compression!
Bonus: a billion strings
The amount of compression one can get from automata can be absolutely
ridiuclous. Consider the particular case of storing all billion strings
in the range 0000000001-1000000000, e.g.,
0000000001
0000000002
...
0000000100
0000000101
...
0999999999
1000000000
The corresponding automaton looks like this:
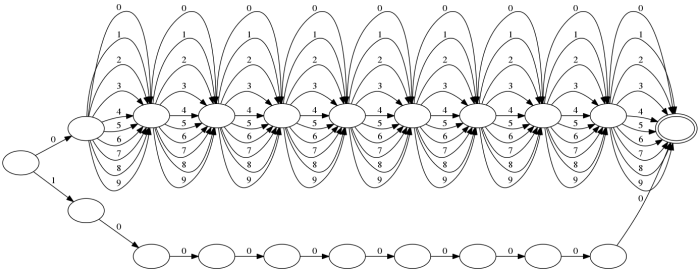
Indeed, the on disk size of this automaton is a mere 251 bytes.
Of course, this is a bit of a pathological best case, but it does serve to show how good compression can be in the optimal case.
Also, check out the corresponding transducer that maps each string to its integer value. It's a bit bigger, but still only takes up 896 bytes of space on disk. This demonstrates that output values are also compressible.
Does this crate produce minimal transducers?
For any non-trivial sized set of keys, it is unlikely that this crate will produce a minimal transducer. As far as this author knows, guaranteeing a minimal transducer requires working memory proportional to the number of states. This can be quite costly and is anathema to the main design goal of this crate: provide the ability to work with gigantic sets of strings with constant memory overhead.
Instead, construction of a finite state transducer uses a cache of states. More frequently used states are cached and reused, which provides reasonably good compression ratios. (No comprehensive benchmarks exist to back up this claim.)
It is possible that this crate may expose a way to guarantee minimal construction of transducers at the expense of exorbitant memory requirements.
Bibliography
I initially got the idea to use finite state tranducers to represent ordered sets/maps from Michael McCandless' work on incorporating transducers in Lucene.
However, my work would also not have been possible without the hard work of many academics, especially Jan Daciuk.
- Incremental construction of minimal acyclic finite-state automata
(Section 3 provides a decent overview of the algorithm used to construct
transducers in this crate, assuming all outputs are
0.) - Direct Construction of Minimal Acyclic Subsequential Transducers (The whole thing. The proof is dense but illuminating. The algorithm at the end is the money shot, namely, it incorporates output values.)
- Experiments with Automata Compression, Smaller Representation of Finite State Automata (various compression techniques for representing states/transitions)
- Jan Daciuk's dissertation (excellent for in depth overview)
- Comparison of Construction Algorithms for Minimal, Acyclic, Deterministic, Finite-State Automata from Sets of Strings (excellent for surface level overview)
Implementations
impl Fst<Vec<u8>>[src]
pub fn from_iter_set<K, I>(iter: I) -> Result<Fst<Vec<u8>>> where
K: AsRef<[u8]>,
I: IntoIterator<Item = K>, [src]
K: AsRef<[u8]>,
I: IntoIterator<Item = K>,
Create a new FST from an iterator of lexicographically ordered byte
strings. Every key's value is set to 0.
If the iterator does not yield values in lexicographic order, then an error is returned.
Note that this is a convenience function to build an FST in memory.
To build an FST that streams to an arbitrary io::Write, use
raw::Builder.
pub fn from_iter_map<K, I>(iter: I) -> Result<Fst<Vec<u8>>> where
K: AsRef<[u8]>,
I: IntoIterator<Item = (K, u64)>, [src]
K: AsRef<[u8]>,
I: IntoIterator<Item = (K, u64)>,
Create a new FST from an iterator of lexicographically ordered byte strings. The iterator should consist of tuples, where the first element is the byte string and the second element is its corresponding value.
If the iterator does not yield unique keys in lexicographic order, then an error is returned.
Note that this is a convenience function to build an FST in memory.
To build an FST that streams to an arbitrary io::Write, use
raw::Builder.
impl<D: AsRef<[u8]>> Fst<D>[src]
pub fn new(data: D) -> Result<Fst<D>>[src]
Creates a transducer from its representation as a raw byte sequence.
This operation is intentionally very cheap (no allocations and no
copies). In particular, no verification on the integrity of the
FST is performed. Callers may opt into integrity checks via the
Fst::verify method.
The fst must have been written with a compatible finite state
transducer builder (Builder qualifies). If the format is invalid or
if there is a mismatch between the API version of this library and the
fst, then an error is returned.
pub fn get<B: AsRef<[u8]>>(&self, key: B) -> Option<Output>[src]
Retrieves the value associated with a key.
If the key does not exist, then None is returned.
pub fn contains_key<B: AsRef<[u8]>>(&self, key: B) -> bool[src]
Returns true if and only if the given key is in this FST.
pub fn get_key(&self, value: u64) -> Option<Vec<u8>>[src]
Retrieves the key associated with the given value.
This is like get_key_into, but will return the key itself without
allowing the caller to reuse an allocation.
If the given value does not exist, then None is returned.
The values in this FST are not monotonically increasing when sorted lexicographically by key, then this routine has unspecified behavior.
pub fn get_key_into(&self, value: u64, key: &mut Vec<u8>) -> bool[src]
Retrieves the key associated with the given value.
If the given value does not exist, then false is returned. In this
case, the contents of key are unspecified.
The given buffer is not clearer before the key is written to it.
The values in this FST are not monotonically increasing when sorted lexicographically by key, then this routine has unspecified behavior.
pub fn stream(&self) -> Stream[src]
Return a lexicographically ordered stream of all key-value pairs in this fst.
pub fn range(&self) -> StreamBuilder[src]
Return a builder for range queries.
A range query returns a subset of key-value pairs in this fst in a range given in lexicographic order.
pub fn search<A: Automaton>(&self, aut: A) -> StreamBuilder<A>[src]
Executes an automaton on the keys of this FST.
pub fn search_with_state<A: Automaton>(
&self,
aut: A
) -> StreamWithStateBuilder<A>[src]
&self,
aut: A
) -> StreamWithStateBuilder<A>
Executes an automaton on the keys of this FST and yields matching keys along with the corresponding matching states in the given automaton.
pub fn len(&self) -> usize[src]
Returns the number of keys in this fst.
pub fn is_empty(&self) -> bool[src]
Returns true if and only if this fst has no keys.
pub fn size(&self) -> usize[src]
Returns the number of bytes used by this fst.
pub fn verify(&self) -> Result<()>[src]
Attempts to verify this FST by computing its checksum.
This will scan over all of the bytes in the underlying FST, so this may be an expensive operation depending on the size of the FST.
This returns an error in two cases:
- When a checksum does not exist, which is the case for FSTs that were
produced by the
fstcrate before version0.4. - When the checksum in the FST does not match the computed checksum performed by this procedure.
pub fn op(&self) -> OpBuilder[src]
Creates a new fst operation with this fst added to it.
The OpBuilder type can be used to add additional fst streams
and perform set operations like union, intersection, difference and
symmetric difference on the keys of the fst. These set operations also
allow one to specify how conflicting values are merged in the stream.
pub fn is_disjoint<'f, I, S>(&self, stream: I) -> bool where
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>, [src]
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>,
Returns true if and only if the self fst is disjoint with the fst
stream.
stream must be a lexicographically ordered sequence of byte strings
with associated values.
pub fn is_subset<'f, I, S>(&self, stream: I) -> bool where
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>, [src]
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>,
Returns true if and only if the self fst is a subset of the fst
stream.
stream must be a lexicographically ordered sequence of byte strings
with associated values.
pub fn is_superset<'f, I, S>(&self, stream: I) -> bool where
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>, [src]
I: for<'a> IntoStreamer<'a, Into = S, Item = (&'a [u8], Output)>,
S: 'f + for<'a> Streamer<'a, Item = (&'a [u8], Output)>,
Returns true if and only if the self fst is a superset of the fst
stream.
stream must be a lexicographically ordered sequence of byte strings
with associated values.
pub fn fst_type(&self) -> FstType[src]
Returns the underlying type of this fst.
FstType is a convention used to indicate the type of the underlying transducer.
This crate reserves the range 0-255 (inclusive) but currently leaves the meaning of 0-255 unspecified.
pub fn root(&self) -> Node[src]
Returns the root node of this fst.
pub fn node(&self, addr: CompiledAddr) -> Node[src]
Returns the node at the given address.
Node addresses can be obtained by reading transitions on Node values.
pub fn to_vec(&self) -> Vec<u8>[src]
Returns a copy of the binary contents of this FST.
pub fn as_bytes(&self) -> &[u8][src]
Returns the binary contents of this FST.
impl<D> Fst<D>[src]
pub fn into_inner(self) -> D[src]
Returns the underlying data which constitutes the FST itself.
pub fn map_data<F, T>(self, f: F) -> Result<Fst<T>> where
F: FnMut(D) -> T,
T: AsRef<[u8]>, [src]
F: FnMut(D) -> T,
T: AsRef<[u8]>,
Maps the underlying data of the fst to another data type.
Trait Implementations
impl<D: AsRef<[u8]>> AsRef<Fst<D>> for Map<D>[src]
Returns the underlying finite state transducer.
impl<D: AsRef<[u8]>> AsRef<Fst<D>> for Set<D>[src]
Returns the underlying finite state transducer.
impl<D: Clone> Clone for Fst<D>[src]
impl<D: AsRef<[u8]>> From<Fst<D>> for Map<D>[src]
impl<D: AsRef<[u8]>> From<Fst<D>> for Set<D>[src]
impl<'a, 'f, D: AsRef<[u8]>> IntoStreamer<'a> for &'f Fst<D>[src]
Auto Trait Implementations
impl<D> RefUnwindSafe for Fst<D> where
D: RefUnwindSafe,
D: RefUnwindSafe,
impl<D> Send for Fst<D> where
D: Send,
D: Send,
impl<D> Sync for Fst<D> where
D: Sync,
D: Sync,
impl<D> Unpin for Fst<D> where
D: Unpin,
D: Unpin,
impl<D> UnwindSafe for Fst<D> where
D: UnwindSafe,
D: UnwindSafe,
Blanket Implementations
impl<T> Any for T where
T: 'static + ?Sized, [src]
T: 'static + ?Sized,
impl<T> Borrow<T> for T where
T: ?Sized, [src]
T: ?Sized,
impl<T> BorrowMut<T> for T where
T: ?Sized, [src]
T: ?Sized,
fn borrow_mut(&mut self) -> &mut T[src]
impl<T> From<T> for T[src]
impl<T, U> Into<U> for T where
U: From<T>, [src]
U: From<T>,
impl<T> ToOwned for T where
T: Clone, [src]
T: Clone,
type Owned = T
The resulting type after obtaining ownership.
fn to_owned(&self) -> T[src]
fn clone_into(&self, target: &mut T)[src]
impl<T, U> TryFrom<U> for T where
U: Into<T>, [src]
U: Into<T>,
type Error = Infallible
The type returned in the event of a conversion error.
fn try_from(value: U) -> Result<T, <T as TryFrom<U>>::Error>[src]
impl<T, U> TryInto<U> for T where
U: TryFrom<T>, [src]
U: TryFrom<T>,