Expand description
Fast evaluation of algebraic expressions
§Features
- No dependencies.
- Safe execution of untrusted expressions.
- Works with stable Rust.
- Supports interpretation (i.e. parse & eval) as well as compiled execution (i.e. parse, compile, eval).
- Supports Variables and Custom Functions.
fastevalis a good base for building higher-level languages.- Supports many built-in functions and constants.
- Supports all the standard algebraic unary and binary operators (+ - * / ^ %), as well as comparisons (< <= == != >= >) and logical operators (&& ||) with short-circuit support.
- Easy integration into many different types of applications, including scoped evaluation.
- Very fast performance.
§The fasteval Expression “Mini-Language”
§Built-in Functions and Constants
These are the built-in functions that fasteval expressions support. (You
can also add your own custom functions and variables – see the
Examples section.)
* print(...strings and values...) -- Prints to stderr. Very useful to 'probe' an expression.
Evaluates to the last value.
Example: `print("x is", x, "and y is", y)`
Example: `x + print("y:", y) + z == x+y+z`
* log(base=10, val) -- Logarithm with optional 'base' as first argument.
If not provided, 'base' defaults to '10'.
Example: `log(100) + log(e(), 100)`
* e() -- Euler's number (2.718281828459045)
* pi() -- π (3.141592653589793)
* int(val)
* ceil(val)
* floor(val)
* round(modulus=1, val) -- Round with optional 'modulus' as first argument.
Example: `round(1.23456) == 1 && round(0.001, 1.23456) == 1.235`
* abs(val)
* sign(val)
* min(val, ...) -- Example: `min(1, -2, 3, -4) == -4`
* max(val, ...) -- Example: `max(1, -2, 3, -4) == 3`
* sin(radians) * asin(val)
* cos(radians) * acos(val)
* tan(radians) * atan(val)
* sinh(val) * asinh(val)
* cosh(val) * acosh(val)
* tanh(val) * atanh(val)§Operators
The and and or operators are enabled by default, but if your
application wants to use those words for something else, they can be
disabled by turning off the alpha-keywords feature (cargo build --no-default-features).
Listed in order of precedence:
(Highest Precedence) ^ Exponentiation
% Modulo
/ Division
* Multiplication
- Subtraction
+ Addition
== != < <= >= > Comparisons (all have equal precedence)
&& and Logical AND with short-circuit
(Lowest Precedence) || or Logical OR with short-circuit
§Numeric Literals
Several numeric formats are supported:
Integers: 1, 2, 10, 100, 1001
Decimals: 1.0, 1.23456, 0.000001
Exponents: 1e3, 1E3, 1e-3, 1E-3, 1.2345e100
Suffix:
1.23p = 0.00000000000123
1.23n = 0.00000000123
1.23µ, 1.23u = 0.00000123
1.23m = 0.00123
1.23K, 1.23k = 1230
1.23M = 1230000
1.23G = 1230000000
1.23T = 1230000000000§Examples
§Easy evaluation
The ez_eval() function performs the entire allocation-parse-eval process
for you. It is slightly inefficient because it always allocates a
fresh Slab, but it is very simple to use:
// In case you didn't know, Rust allows `main()` to return a `Result`.
// This lets us use the `?` operator inside of `main()`. Very convenient!
fn main() -> Result<(), fasteval::Error> {
// This example doesn't use any variables, so just use an EmptyNamespace:
let mut ns = fasteval::EmptyNamespace;
let val = fasteval::ez_eval(
"1+2*3/4^5%6 + log(100K) + log(e(),100) + [3*(3-3)/3] + (2<3) && 1.23", &mut ns)?;
// | | | | | | | |
// | | | | | | | boolean logic with short-circuit support
// | | | | | | comparisons
// | | | | | square-brackets act like parenthesis
// | | | | built-in constants: e(), pi()
// | | | 'log' can take an optional first 'base' argument, defaults to 10
// | | numeric literal with suffix: p, n, µ, m, K, M, G, T
// | many built-in functions: print, int, ceil, floor, abs, sign, log, round, min, max, sin, asin, ...
// standard binary operators
assert_eq!(val, 1.23);
Ok(())
}§Simple variables
Several namespace types are supported, each designed for different situations.
(See the various Namespace types here.) For simple cases, you can define variables with a
BTreeMap:
use std::collections::BTreeMap;
fn main() -> Result<(), fasteval::Error> {
let mut map : BTreeMap<String,f64> = BTreeMap::new();
map.insert("x".to_string(), 1.0);
map.insert("y".to_string(), 2.0);
map.insert("z".to_string(), 3.0);
let val = fasteval::ez_eval(r#"x + print("y:",y) + z"#, &mut map)?;
// |
// prints "y: 2" to stderr and then evaluates to 2.0
assert_eq!(val, 6.0);
Ok(())
}§Advanced variables and custom functions
This time, instead of using a map, we will use a callback function, which defines custom variables, functions, and array-like objects:
fn main() -> Result<(), fasteval::Error> {
let mut cb = |name:&str, args:Vec<f64>| -> Option<f64> {
let mydata : [f64; 3] = [11.1, 22.2, 33.3];
match name {
// Custom constants/variables:
"x" => Some(3.0),
"y" => Some(4.0),
// Custom function:
"sum" => Some(args.into_iter().sum()),
// Custom array-like objects:
// The `args.get...` code is the same as:
// mydata[args[0] as usize]
// ...but it won't panic if either index is out-of-bounds.
"data" => args.get(0).and_then(|f| mydata.get(*f as usize).copied()),
// A wildcard to handle all undefined names:
_ => None,
}
};
let val = fasteval::ez_eval("sum(x^2, y^2)^0.5 + data[0]", &mut cb)?;
// | | |
// | | square-brackets act like parenthesis
// | variables are like custom functions with zero args
// custom function
assert_eq!(val, 16.1);
// Let's explore some of the hidden complexities of variables:
//
// * There's really no difference between a variable and a custom function.
// Therefore, variables can receive arguments too,
// which will probably be ignored.
// Therefore, these two expressions evaluate to the same thing:
// eval("x + y") == eval("x(1,2,3) + y(x, y, sum(x,y))")
// ^^^^^ ^^^^^^^^^^^^^^
// All this stuff is ignored.
//
// * Built-in functions take precedence WHEN CALLED AS FUNCTIONS.
// This design was chosen so that builtin functions do not pollute
// the variable namespace, which is important for some applications.
// Here are some examples:
// pi -- Uses the custom 'pi' variable, NOT the builtin 'pi' function.
// pi() -- Uses the builtin 'pi' function even if a custom variable is defined.
// pi(1,2,3) -- Uses the builtin 'pi' function, and produces a WrongArgs error
// during parse because the builtin does not expect any arguments.
// x -- Uses the custom 'x' variable.
// x() -- Uses the custom 'x' variable because there is no 'x' builtin.
// x(1,2,3) -- Uses the custom 'x' variable. The args are ignored.
// sum -- Uses the custom 'sum' function with no arguments.
// sum() -- Uses the custom 'sum' function with no arguments.
// sum(1,2) -- Uses the custom 'sum' function with two arguments.
Ok(())
}§Re-use the Slab to go faster
If we perform the parse and eval ourselves (without relying on the ‘ez’
interface), then we can re-use the Slab allocation for
subsequent parsing and evaluations. This avoids a significant amount of
slow memory operations:
use std::collections::BTreeMap;
use fasteval::Evaler; // use this trait so we can call eval().
fn main() -> Result<(), fasteval::Error> {
let parser = fasteval::Parser::new();
let mut slab = fasteval::Slab::new();
// See the `parse` documentation to understand why we use `from` like this:
let expr_ref = parser.parse("x + 1", &mut slab.ps)?.from(&slab.ps);
// Let's evaluate the expression a couple times with different 'x' values:
let mut map : BTreeMap<String,f64> = BTreeMap::new();
map.insert("x".to_string(), 1.0);
let val = expr_ref.eval(&slab, &mut map)?;
assert_eq!(val, 2.0);
map.insert("x".to_string(), 2.5);
let val = expr_ref.eval(&slab, &mut map)?;
assert_eq!(val, 3.5);
// Now, let's re-use the Slab for a new expression.
// (This is much cheaper than allocating a new Slab.)
// The Slab gets cleared by 'parse()', so you must avoid using
// the old expr_ref after parsing the new expression.
// One simple way to avoid this problem is to shadow the old variable:
let expr_ref = parser.parse("x * 10", &mut slab.ps)?.from(&slab.ps);
let val = expr_ref.eval(&slab, &mut map)?;
assert_eq!(val, 25.0);
Ok(())
}§Compile to go super fast!
If you plan to evaluate an expression just one or two times, then you should parse-eval as shown in previous examples. But if you expect to evaluate an expression three or more times, you can dramatically improve your performance by compiling. The compiled form is usually more than 10 times faster than the un-compiled form, and for constant expressions it is usually more than 200 times faster.
use std::collections::BTreeMap;
use fasteval::Evaler; // use this trait so we can call eval().
use fasteval::Compiler; // use this trait so we can call compile().
fn main() -> Result<(), fasteval::Error> {
let parser = fasteval::Parser::new();
let mut slab = fasteval::Slab::new();
let mut map = BTreeMap::new();
let expr_str = "sin(deg/360 * 2*pi())";
let compiled = parser.parse(expr_str, &mut slab.ps)?.from(&slab.ps).compile(&slab.ps, &mut slab.cs);
for deg in 0..360 {
map.insert("deg".to_string(), deg as f64);
// When working with compiled constant expressions, you can use the
// eval_compiled*!() macros to save a function call:
let val = fasteval::eval_compiled!(compiled, &slab, &mut map);
eprintln!("sin({}°) = {}", deg, val);
}
Ok(())
}§Unsafe Variables
If your variables must be as fast as possible and you are willing to be
very careful, you can build with the unsafe-vars feature (cargo build --features unsafe-vars), which enables pointer-based variables. These
unsafe variables perform 2x-4x faster than the compiled form above. This
feature is not enabled by default because it slightly slows down other
non-variable operations.
use fasteval::Evaler; // use this trait so we can call eval().
use fasteval::Compiler; // use this trait so we can call compile().
fn main() -> Result<(), fasteval::Error> {
let parser = fasteval::Parser::new();
let mut slab = fasteval::Slab::new();
// The Unsafe Variable will use a pointer to read this memory location:
// You must make sure that this variable stays in-scope as long as the
// expression is in-use.
let mut deg : f64 = 0.0;
// Unsafe Variables must be registered before 'parse()'.
// (Normal Variables only need definitions during the 'eval' phase.)
unsafe { slab.ps.add_unsafe_var("deg".to_string(), °); } // `add_unsafe_var()` only exists if the `unsafe-vars` feature is enabled: `cargo test --features unsafe-vars`
let expr_str = "sin(deg/360 * 2*pi())";
let compiled = parser.parse(expr_str, &mut slab.ps)?.from(&slab.ps).compile(&slab.ps, &mut slab.cs);
let mut ns = fasteval::EmptyNamespace; // We only define unsafe variables, not normal variables,
// so EmptyNamespace is fine.
for d in 0..360 {
deg = d as f64;
let val = fasteval::eval_compiled!(compiled, &slab, &mut ns);
eprintln!("sin({}°) = {}", deg, val);
}
Ok(())
}§Let’s Develop an Intuition of fasteval Internals
In this advanced example, we peek into the Slab to see how expressions are represented after the ‘parse’ and ‘compile’ phases.
use fasteval::Compiler; // use this trait so we can call compile().
fn main() -> Result<(), fasteval::Error> {
let parser = fasteval::Parser::new();
let mut slab = fasteval::Slab::new();
let expr_str = "sin(deg/360 * 2*pi())";
let expr_ref = parser.parse(expr_str, &mut slab.ps)?.from(&slab.ps);
// Let's take a look at the parsed AST inside the Slab:
// If you find this structure confusing, take a look at the compilation
// AST below because it is simpler.
assert_eq!(format!("{:?}", slab.ps),
r#"ParseSlab{ exprs:{ 0:Expression { first: EStdFunc(EVar("deg")), pairs: [ExprPair(EDiv, EConstant(360.0)), ExprPair(EMul, EConstant(2.0)), ExprPair(EMul, EStdFunc(EFuncPi))] }, 1:Expression { first: EStdFunc(EFuncSin(ExpressionI(0))), pairs: [] } }, vals:{} }"#);
// Pretty-Print:
// ParseSlab{
// exprs:{
// 0:Expression { first: EStdFunc(EVar("deg")),
// pairs: [ExprPair(EDiv, EConstant(360.0)),
// ExprPair(EMul, EConstant(2.0)),
// ExprPair(EMul, EStdFunc(EFuncPi))]
// },
// 1:Expression { first: EStdFunc(EFuncSin(ExpressionI(0))),
// pairs: [] }
// },
// vals:{}
// }
let compiled = expr_ref.compile(&slab.ps, &mut slab.cs);
// Let's take a look at the compilation results and the AST inside the Slab:
// Notice that compilation has performed constant-folding: 1/360 * 2*pi = 0.017453292519943295
// In the results below: IFuncSin(...) represents the sin function.
// InstructionI(1) represents the Instruction stored at index 1.
// IMul(...) represents the multiplication operator.
// 'C(0.017...)' represents a constant value of 0.017... .
// IVar("deg") represents a variable named "deg".
assert_eq!(format!("{:?}", compiled),
"IFuncSin(InstructionI(1))");
assert_eq!(format!("{:?}", slab.cs),
r#"CompileSlab{ instrs:{ 0:IVar("deg"), 1:IMul(InstructionI(0), C(0.017453292519943295)) } }"#);
Ok(())
}§Safety
fasteval is designed to evaluate untrusted expressions safely. By
default, an expression can only perform math operations; there is no way
for it to access other types of operations (like network or filesystem or
external commands). Additionally, we guard against malicious expressions:
- Expressions that are too large (greater than 4KB).
- Expressions that are too-deeply nested (greater than 32 levels).
- Expressions with too many values (greater than 64).
- Expressions with too many sub-expressions (greater than 64).
All limits can be customized at parse time. If any limits are exceeded,
parse() will return an
Error.
Note that it is possible for you (the developer) to define custom functions which might perform dangerous operations. It is your responsibility to make sure that all custom functionality is safe.
§Performance Benchmarks
These benchmarks were performed on 2019-12-25. Merry Christmas.
Here are links to all the libraries/tools included in these benchmarks:
§Charts
Note that the following charts use logarithmic scales. Therefore, tiny visual differences actually represent very significant performance differences.
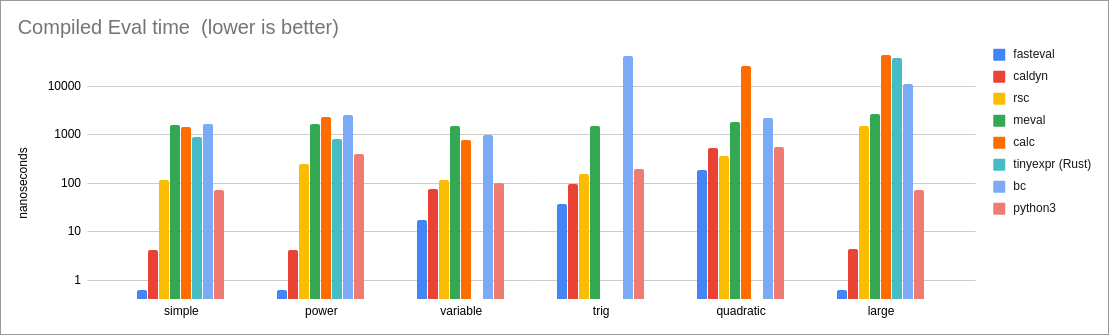
Performance of evaluation of a compiled expression:
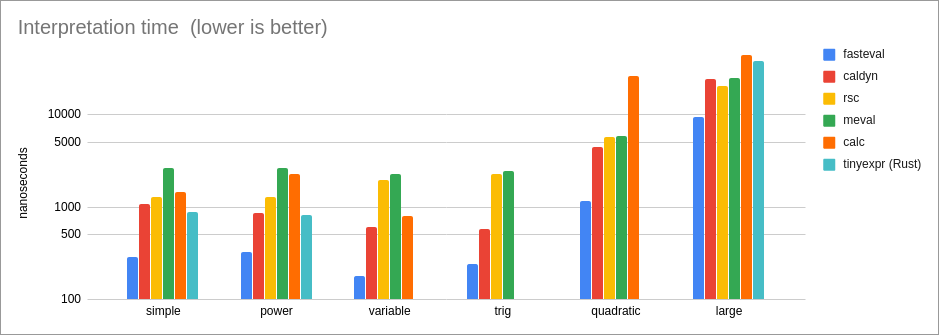
Performance of one-time interpretation (parse and eval):
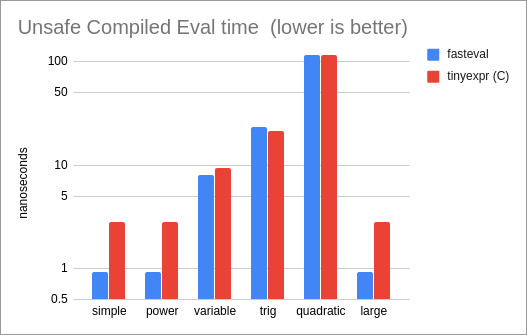
Performance of compiled Unsafe Variables, compared to the tinyexpr C library (the
only other library in our test set that supports this mode):
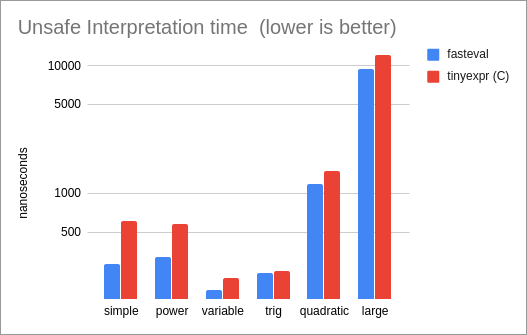
Performance of interpreted Unsafe Variables, compared to the tinyexpr C library (the
only other library in our test set that supports this mode):
§Summary
The impressive thing about these results is that fasteval consistently
achieves the fastest times across every benchmark and in every mode of
operation (interpreted, compiled, and unsafe). It’s easy to create a
design to claim the #1 spot in any one of these metrics by sacrificing
performance in another, but it is difficult to create a design that can be
#1 across-the-board.
Because of the broad and robust performance advantages, fasteval is very
likely to be an excellent choice for your dynamic evaluation needs.
§Benchmark Descriptions & Analysis
* simple = `3 * 3 - 3 / 3`
This is a simple test with primitive binary operators.
Since the expression is quite simple, it does a good job of showing
the intrinsic performance costs of a library.
Results:
* For compiled expressions, `fasteval` is 6x as fast as the closest
competitor (caldyn) because the `eval_compiled!()` macro is able to
eliminate all function calls. If the macro is not used and a
normal `expr.eval()` function call is performed instead, then
performance is very similar to caldyn's.
* For interpreted expressions, `fasteval` is 2x as fast as the
tinyexpr C lib, and 3x as fast as the tinyexpr Rust lib.
This is because `fasteval` eliminates redundant work and memory
allocation during the parse phase.
* power = `2 ^ 3 ^ 4`
`2 ^ (3 ^ 4)` for `tinyexpr` and `rsc`
This test shows the associativity of the exponent operator.
Most libraries (including `fasteval`) use right-associativity,
but some libraries (particularly tinyexpr and rsc) use
left-associativity.
This test is also interesting because it shows the precision of a
library's number system. `fasteval` just uses f64 and therefore truncates
the result (2417851639229258300000000), while python, bc, and the
tinyexpr C library produce a higher precision result
(2417851639229258349412352).
Results:
Same as the 'simple' case.
* variable = `x * 2`
This is a simple test of variable support.
Since the expression is quite simple, it shows the intrinsic
performance costs of a library's variables.
Results:
* The tinyexpr Rust library does not currently support variables.
* For safe compiled evaluation, `fasteval` is 4.4x as fast as the closest
competitor (caldyn).
* For safe interpretation, `fasteval` is 3.3x as fast as the closest
competitor (caldyn).
* For unsafe variables, `fasteval` is 1.2x as fast as the
tinyexpr C library.
* trig = `sin(x)`
This is a test of variables, built-in function calls, and trigonometry.
Results:
* The tinyexpr Rust library does not currently support variables.
* The `calc` library does not support trigonometry.
* For safe compiled evaluation, `fasteval` is 2.6x as fast as the
closest competitor (caldyn).
* For safe interpretation, `fasteval` is 2.3x as fast as the closest
competitor (caldyn).
* Comparing unsafe variables with the tinyexpr C library,
`fasteval` is 8% slower for compiled expressions (tinyexpr uses a
faster `sin` implementation) and 4% faster for interpreted
expressions (`fasteval` performs less memory allocation).
* quadratic = `(-z + (z^2 - 4*x*y)^0.5) / (2*x)`
This test demonstrates a more complex expression, involving several
variables, some of which are accessed more than once.
Results:
* The tinyexpr Rust library does not currently support variables.
* For safe compiled evaluation, `fasteval` is 2x as fast as the
closest competitor (rsc).
* For safe interpretation, `fasteval` is 3.7x as fast as the
closest competitor (caldyn).
* Comparing unsafe variables with the tinyexpr C library,
`fasteval` is the same speed for compiled expressions,
and 1.2x as fast for interpretation.
* large = `((((87))) - 73) + (97 + (((15 / 55 * ((31)) + 35))) + (15 - (9)) - (39 / 26) / 20 / 91 + 27 / (33 * 26 + 28 - (7) / 10 + 66 * 6) + 60 / 35 - ((29) - (69) / 44 / (92)) / (89) + 2 + 87 / 47 * ((2)) * 83 / 98 * 42 / (((67)) * ((97))) / (34 / 89 + 77) - 29 + 70 * (20)) + ((((((92))) + 23 * (98) / (95) + (((99) * (41))) + (5 + 41) + 10) - (36) / (6 + 80 * 52 + (90))))`
This is a fairly large expression that highlights parsing costs.
Results:
* Since there are no variables in the expression, `fasteval` and
`caldyn` compile this down to a single constant value. That's
why these two libraries are so much faster than the rest.
* For compiled evaluation, `fasteval` is 6x as fast as `caldyn`
because it is able to eliminate function calls with the
`eval_compiled!()` macro.
* For interpretation, `fasteval` is 2x as fast as the closest
competitor (rsc).
* Comparing unsafe variables with the tinyexpr C library,
`fasteval` is 3x as fast for compiled evaluation, and
1.2x as fast for interpretation.§Methodology
I am running Ubuntu 18.04 on an Asus G55V (a 2012 laptop with Intel Core i7-3610QM CPU @ 2.3GHz - 3.3GHz).
All numeric results can be found in fasteval/benches/bench.rs.
See the [detailed post about my benchmarking methology]{http://likebike.com/posts/How_To_Write_Fast_Rust_Code.html#how-to-measure} on my blog.
§How is fasteval so fast?
A variety of techniques are used to optimize performance:
- Minimization of memory allocations/deallocations;
I just pre-allocate a large
Slabduring initialization. - Elimination of redundant work, especially when parsing.
- Designed using “Infallible Data Structures”, which eliminate all corner cases.
- Compilation: Constant Folding and Expression Simplification. Boosts performance up to 1000x.
- Profile-driven application of inlining. Don’t inline too much or too little. Maximizes data locality.
- Localize variables. Use
RUSTFLAGS="--emit=asm"as a guide.
§Can fasteval be faster?
Yes, but not easily, and not by much.
To boost the ‘eval’ phase, we would really need to perform compilation to machine code, which is difficult and non-portable across platforms, and increases the likelyhood of security vulnerabilities. Also, the potential gains are limited: We already run at half-the-speed-of-compiled-optimized-Rust for constant expressions (the most common case). So for constant expressions, the most you could gain from compilation-to-machine-code is a 2x performance boost. We are already operating close to the theoretical limit!
It is possible to perform faster evaluation of non-constant expressions by introducing more constraints or complexity:
- If I introduce a ‘const’ var type, then I can transform variable expressions into constant expressions. I don’t think this would be useful-enough in real-life to justify the extra complexity (but please tell me if your use-case would benefit from this).
- Evaluation could be paralellized (with a more complex design).
It is possible to boost overall speed by improving the parsing algorithm to produce a Reverse Polish Notation AST directly, rather than the currennt infix AST which is then converted to RPN during compilation. However, this isn’t as simple as just copying the Shunting-Yard algorithm because I support more advanced (and customizable) syntax (such as function calls and strings), while Shunting-Yard is designed only for algebraic expressions.
§Future Work
Here are some features that I might add in the future:
- Dynamic
sprintfstring formatting for theprint()built-in expression function. - FFI so this library can be used from other languages.
- Ability to copy the contents of a
Slabinto a perfectly-sized container (PackedSlab) to reduce wasted memory. - Support for other number types other than
f64, such as Integers, Big Integers, Arbitrary Precision Numbers, Complex Numbers, etc. like rclc.
§List of Projects that use fasteval
Send me a message if you would like to list your project here.
Re-exports§
pub use self::error::Error;pub use self::parser::Parser;pub use self::parser::Expression;pub use self::parser::ExpressionI;pub use self::parser::Value;pub use self::parser::ValueI;pub use self::compiler::Compiler;pub use self::compiler::Instruction;pub use self::compiler::Instruction::IConst;pub use self::compiler::InstructionI;pub use self::evaler::Evaler;pub use self::slab::Slab;pub use self::evalns::EvalNamespace;pub use self::evalns::Cached;pub use self::evalns::EmptyNamespace;pub use self::evalns::StringToF64Namespace;pub use self::evalns::StrToF64Namespace;pub use self::evalns::StringToCallbackNamespace;pub use self::evalns::StrToCallbackNamespace;pub use self::evalns::LayeredStringToF64Namespace;pub use self::evalns::CachedCallbackNamespace;pub use self::ez::ez_eval;
Modules§
- compiler
- This module compiles parsed
Expressions into an optimized AST node called anInstruction. The compiled form is much faster, especially for constants. - error
- This module contains
fasteval’s Error type: anenumthat contains all errors that can be produced by thefastevalAPI. - evaler
- This module evaluates parsed
Expressions and compiledInstructions. - evalns
- Evaluation Namespaces used for Variable-lookups and custom Functions.
- ez
- An easy API for single-function-call expression evaluation.
- parser
- This module parses string expressions into an AST which can then be compiled or evaluated.
- slab
- A
Slabis a pre-allocated block of memory, used during the parse/compile/eval phases to reduce memory allocation/deallocation.
Macros§
- bool_
to_ f64 true–>1.0,false–>0.0- eval_
compiled - The same as
evaler.eval(&slab, &mut ns), but more efficient for common cases. - eval_
compiled_ ref - The same as
evaler_ref.eval(&slab, &mut ns), but more efficient for common cases. - f64_eq
- Uses
EPSILONto determine equality of twof64s. - f64_ne
- Uses
EPSILONto determine inequality of twof64s.