//! # CipherCore
//!
//! If you have any questions, or, more generally, would like to discuss CipherCore, please [join the Slack community](https://join.slack.com/t/slack-r5s9809/shared_invite/zt-1901t4ec3-W4pk~nsTl2dY8Is5HFWT4w).
//!
//! # Table of contents
//! - [CipherCore](#ciphercore)
//! - [Table of contents](#table-of-contents)
//! - [Overview](#overview)
//!    - [What is CipherCore?](#what-is-ciphercore)
//!    - [What is Secure Computation?](#what-is-secure-computation)
//!    - [CipherCore and Intermediate Representation](#ciphercore-and-intermediate-representation)
//!    - [Bird's eye view of SMPC](#birds-eye-view-of-smpc)
//!       - [Secret sharing](#secret-sharing)
//!    - [High-level structure of CipherCore](#high-level-structure-of-ciphercore)
//!       - [What is CipherCore useful for](#what-is-ciphercore-useful-for)
//! - [System requirements, installation and licensing](#system-requirements-installation-and-licensing)
//! - [Quick start](#quick-start)
//!    - [Creating computation graph](#creating-computation-graph)
//!    - [Working with the graph using CLI tools](#working-with-the-graph-using-cli-tools)
//! - [Examples](#examples)
//!    - [Matrix multiplication](#matrix-multiplication)
//!    - [Millionaires' problem](#millionaires-problem)
//!    - [Minimum of an array](#minimum-of-an-array)
//!    - [Sort](#sort)
//! - [Graph creation and management](#graph-creation-and-management)
//!    - [Overview of CipherCore operations](#overview-of-ciphercore-operations)
//!       - [Data types](#data-types)
//!       - [Basic operations](#basic-operations)
//!       - [Custom operations](#custom-operations)
//! - [CLI Tools](#cli-tools)
//!    - [Compiler](#compiler)
//!    - [Evaluator](#evaluator)
//!       - [Secret-shared input](#secret-shared-input)
//!       - [Input format](#input-format)
//!    - [Visualization](#visualization)
//!    - [Inspection](#inspection)
//!
//! # Overview
//!
//! ## What is CipherCore?
//!
//! CipherCore is a general purpose library for processing encrypted data.
//! It’s a state-of-the-art platform for building customized applications that can run directly over encrypted data without decrypting it first.
//! CipherCore can be used to run tasks on multiple distributed datasets owned by multiple organizations within the same enterprise or even different enterprises without disclosing the data to other parties.
//! The library is based on a technology called secure computation.
//!
//! ## What is Secure Computation?
//!
//! Secure Multi-Party Computation (SMPC) is a cutting-edge subfield of cryptography that provides various types of protocols allowing the execution of certain programs over encrypted data ([read more](https://en.wikipedia.org/wiki/Secure_multi-party_computation)).
//! SMPC protocols take as input a restricted form of computation called [circuit representation](https://en.wikipedia.org/wiki/Boolean_circuit).
//! Translating high-level programs into circuit representation is a complicated, error-prone and time-consuming process.
//! CipherCore compiler drastically simplifies the process by automatically translating and compiling high-level programs directly into the SMPC protocols, thus, allowing any software developer to use secure computation without requiring any knowledge of cryptography.
//!
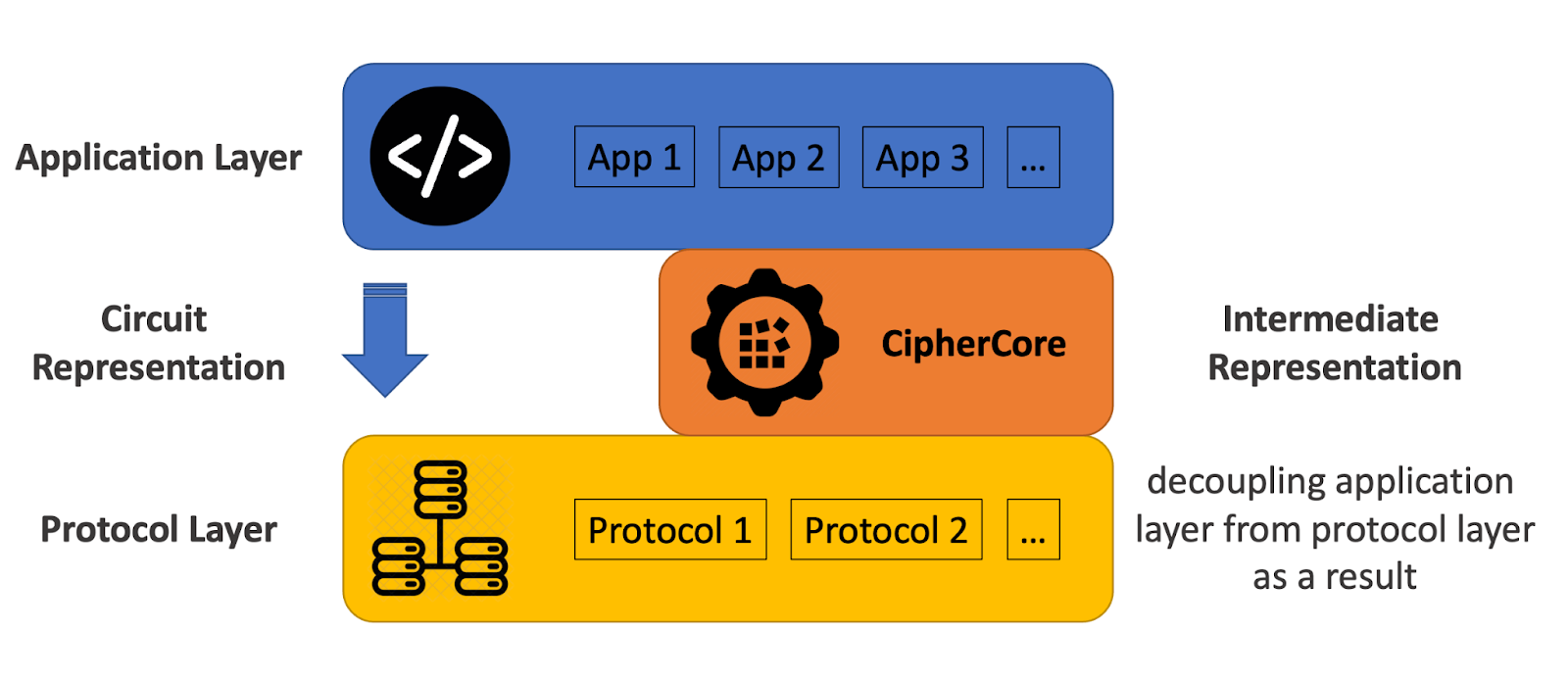
//! ## CipherCore and Intermediate Representation
//!
//! CipherCore’s ease of use is due to introducing a new intermediate representation layer of _computation graphs_ between the application layer and the protocol layer.
//! Applications are mapped to a computation graph first and then to an SMPC protocol.
//! This architecture allows for rapid integration of various SMPC protocols as new cryptographic backends.
//! If you are familiar with ML frameworks such as [PyTorch](https://pytorch.org/), [TensorFlow](https://www.tensorflow.org/) or [JAX](https://github.com/google/jax) (or [MLIR](https://mlir.llvm.org/) on a lower level), then you likely know what computation graphs are.
//!
//! ![CipherCore architecture](https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/ciphercore_architecture.png)
//!
//! ## Bird's eye view of SMPC
//!
//! At a high level, Secure Multi-Party Computation protocols (SMPC) allow, given a program with several inputs belonging to several parties, execute it in a way such that:
//! * The output gets revealed only to a desired set of the parties;
//! * No party learns anything about inputs belonging to other parties other than what can be inferred from the revealed outputs.
//!
//! The literature on SMPC is vast and we refer the reader to a [comprehensive overview](https://github.com/rdragos/awesome-mpc) of the existing protocols. Typically, there is a three-way trade-off between:
//! * Efficiency
//! * Number of parties
//! * Threat model
//!
//! CipherCore is designed in a way that allows most existing SMPC protocols to be readily plugged as a backend.
//! Currently, we support [the ABY3 SMPC protocol](https://eprint.iacr.org/2018/403.pdf), which works for three parties and is one of the most efficient available protocols.
//!
//! ### Secret sharing
//!
//! Often, typically as a part of a larger computation, we need to run SMPC protocol on *secret* inputs that no single party is supposed to know. This can be achieved using a technique called *secret sharing*.
//!
//! The ABY3 protocol uses *replicated secret sharing*.
//! Specifically, a secret value `v` is presented in the form of a triple `(v_0, v_1, v_2)` such that `v = v_0 + v_1 + v_2` and each party has only two components of this triple, namely:
//! * Party 0 holds `(v_0, v_1)`,
//! * Party 1 holds `(v_1, v_2)`,
//! * Party 2 holds `(v_2, v_0)`.
//!
//! Each pair individually is fully random and carries no information about `v`, but, if brought together, the triple allows to recover the secret value.
//!
//! Public values are not secret shared, i.e., each party has a copy of a public value locally. Also, if we want to keep the result of the computation, then it can be maintained in the above secret shared form.
//!
//! ## High-level structure of CipherCore
//!
//! There are four natural stages when working with CipherCore:
//! 1. Formulate a computation one wishes to run securely as a computation graph using graph building API;
//! 2. **Compile** the graph into a new, typically larger, computation graph that corresponds to an SMPC protocol that performs the same computation but, at the same time, preserves the privacy of inputs and outputs. This step can be done using the CipherCore **compiler** that is part of the repository. Currently, we only support the ABY3 SMPC protocol for three non-colluding parties, but this will likely change in the future.
//! 3. Check that the resulting secure protocol works correctly. This can be done by running it on sample inputs using a **local evaluator**. This repository contains a reference implementation of an evaluator, which is simple, but not efficient. We also provide access to a Docker image that contains a binary of a **fast evaluator**, which is typically several orders of magnitude more efficient. The performance of the fast evaluator is a strong predictor (modulo network interactions) of actual end-to-end secure protocol execution done by three distributed parties;
//! 4. Execute the secure protocol end-to-end by three actual distributed parties that interact over the network. This can be done using the CipherCore **runtime**. We provide the trial access to the runtime on request. (see [here](#system-requirements-installation-and-licensing) for details)
//!
//! ### What is CipherCore useful for
//!
//! For an overview of instructions supported by CipherCore, see [here](#overview-of-ciphercore-operations).
//!
//! At a high level, CipherCore operations are designed to support most of the popular machine learning (ML training and inference) and analytics (e.g., [private set intersection](https://en.wikipedia.org/wiki/Private_set_intersection) and, more generally, joins) workloads.
//!
//! Going further, we plan to release **SecureAI**, which transforms popular ONNX graphs obtained from ML models into CipherCore graphs, which are in turn amenable to the SMPC compilation.
//!
//! # System requirements, installation and licensing
//!
//! CipherCore consists of three major parts:
//! * API for building and working with computation graphs;
//! * CLI tools that include the compiler and the evaluator;
//! * The Runtime that executes compiled computation graphs of secure protocols between several distributed parties.
//!
//! This crate can be used both as dependencies within your Rust projects and as a way to install the CLI tools.
//! For the former, add `ciphercore-base` to the dependencies of your Rust project, for the latter, run `cargo install ciphercore-base`.
//! We support most Linux and macOS systems (as well as Windows via WSL) with an Intel CPU.
//! For the crates to build, we require a system-wide install of [OpenSSL](https://www.openssl.org/) discoverable by the Rust [`openssl` crate](https://docs.rs/openssl/latest/openssl/) (the latter typically means the availability of [pkg-config](https://en.wikipedia.org/wiki/Pkg-config)).
//!
//! In addition, you can check out the Python package for the computation graph building API and the Docker image with pre-installed Python package and CLI tools including the *fast evaluator*, whose source code is *not* available in this repository.
//! More information about these parts of CipherCore can be found in [the CipherCore GitHub repo](https://github.com/ciphermodelabs/ciphercore).
//!
//! Everything provided in this repository is licensed under the [Apache 2.0 license](https://github.com/ciphermodelabs/ciphercore/blob/main/LICENSE.txt).
//!
//! If you download and run fast evaluator, you agree with the [CipherMode EULA](https://github.com/ciphermodelabs/EULA/blob/main/CipherMode%20Labs%20Inc.%20EULA%20(Version%2005-03-22).pdf).
//!
//! To request the trial access to the CipherCore Runtime, [e-mail us](mailto:ciphercore@ciphermode.tech).
//!
//! # Quick start
//!
//! Let us consider the following secure computation problem that involves three parties, which we denote by 0, 1, and 2.
//! Party 0 and party 1 each have a 5x5 square matrix with integer entries.
//! The parties would like to multiply these matrices and reveal the result to party 2 in a way that parties 0 and 1 learn nothing about each other's inputs, and party 2 learns nothing about the inputs other than their product.
//! Let us show how this problem can be solved using CipherCore.
//!
//! We need to start with creating a computation graph for the above problem.
//!
//! ## Creating computation graph
//!
//! We assume that you already have Rust and Cargo installed: please refer to the [Rust website](https://www.rust-lang.org/learn/get-started) for the installation instructions.
//!
//! First, let's create a new Rust project as follows: `cargo new private_matrix_multiplication`. Next, go to the project's directory: `cd private_matrix_multiplication`. Then, you need to add the crates `ciphercore-base` and `serde_json` as dependencies (we need the latter for serialization). In order to do this, please make the `Cargo.toml` file look like this:
//! ```toml
//! [package]
//! name = "private_matrix_multiplication"
//! version = "0.1.0"
//! edition = "2021"
//!
//! [dependencies]
//! ciphercore-base = "0.1.0"
//! serde_json = "1.0.81"
//! ```
//!
//! Now, replace the contents of `src/main.rs` with the following:
//!
//! ```no_run
//! use ciphercore_base::graphs::create_context;
//! use ciphercore_base::data_types::{array_type, INT64};
//! use ciphercore_base::errors::Result;
//!
//! fn main() {
//!     || -> Result<()> {
//!         // Create a context that hosts our computation graph.
//!         let context = create_context()?;
//!         // Create our graph within the context.
//!         let graph = context.create_graph()?;
//!         // Create two input nodes that correspond to 5x5
//!         // matrix with signed 64-bit integer entries.
//!         let a = graph.input(array_type(vec![5, 5], INT64))?;
//!         let b = graph.input(array_type(vec![5, 5], INT64))?;
//!         // Create a node that computes the product of `a`
//!         // and `b`.
//!         let c = a.matmul(b)?;
//!         // Declare `c` to be the final result
//!         // of computation.
//!         graph.set_output_node(c)?;
//!         // Freeze the graph thus declaring it to be final.
//!         graph.finalize()?;
//!         // Set `graph` as the main graph of the context.
//!         context.set_main_graph(graph)?;
//!         // Finalize the context.
//!         context.finalize()?;
//!         // Print the serialized context to stdout.
//!         println!("{}", serde_json::to_string(&context)?);
//!         Ok(())
//!     }().unwrap();
//! }
//! ```
//!
//! Next, let's build our project by running `cargo build --release`.
//! Finally, let us generate the graph and serialize it to the file `a.json` as follows: `./target/release/private_matrix_multiplication > a.json`.
//!
//! ## Working with the graph using CLI tools
//!
//! To work with the computation graph, we need to install CLI tools provided with CipherCore by running `cargo install ciphercore-base`.
//! This assumes you have Rust and Cargo installed: please refer to the [Rust website](https://www.rust-lang.org/learn/get-started) for the installation instructions.
//!
//! We can visualize the computation graph we just created as follows (this assumes that [GraphViz](https://graphviz.org/) is installed):
//! ```bash
//! ciphercore_visualize_context a.json | dot -Tsvg -o a.svg
//! ```
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/tutorial_graph_plain.svg" alt="Plain Graph" width="30%"/>
//! </p>
//!
//! So far, nothing outstanding has happened. The graph simply has two input nodes that correspond to the input matrices, and the output node that corresponds to their produce.
//! Each node of the graph has a _type_ associated with it, which is depicted on the image.
//! These types are inferred automatically during the graph construction.
//!
//! Now let us compile the computation graph and turn it into a secure protocol. For this we run:
//! ```bash
//! ciphercore_compile a.json simple 0,1 2 > b.json
//! ```
//!
//! Here, the parameters `0,1 2` means that the inputs belong to the parties 0 and 1, respectively, and the output needs to be revealed only to the party 2.
//!
//! If we visualize the resulting computation graph of the secure protocol, we get the following:
//!
//! ```bash
//! ciphercore_visualize_context b.json | dot -Tsvg -o b.svg
//! ```
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/tutorial_graph_mpc.svg" alt="MPC Graph" width="40%"/>
//! </p>
//!
//! As one can see, the compiled graph is much more complicated: in particular, it contains nodes that call a [cryptographic pseudo-random generator](https://en.wikipedia.org/wiki/Pseudorandom_generator), [cryptographic pseudo-random function](https://en.wikipedia.org/wiki/Pseudorandom_function_family) as well as nodes that correspond to network interactions between the parties.
//!
//! We can gather the statistics of the compiled graph as follows: `ciphercore_inspect b.json` and get the following:
//! ```bash
//! -------Stats--------
//! Inputs:
//!     1. Name:unnamed
//!     Type:i64[5, 5]
//!     2. Name:unnamed
//!     Type:i64[5, 5]
//! Output:
//!     Name:unnamed
//!     Type:i64[5, 5]
//! Network rounds: 4
//! Network traffic: 2.00KB
//! Total number of integer arithmetic operations:   2.84K Ops
//!     Total number of 1-bit arithmetic operations:   384 Ops
//!     Total number of 8-bit arithmetic operations:   0 Ops
//!     Total number of 16-bit arithmetic operations:  0 Ops
//!     Total number of 32-bit arithmetic operations:  0 Ops
//!     Total number of 64-bit arithmetic operations:  2.45K Ops
//! Total operations: 55
//! Operations:
//!     NOP           13
//!     Add           13
//!     Subtract      9
//!     PRF           9
//!     Matmul        6
//!     Random        3
//!     Input         2
//! ```
//! Let us note that the compiled graph has exactly the same matrix multiplication functionality as the original graph, but it gives a blueprint of the secure protocol.
//! That is, if three non-colluding parties faithfully execute the compiled graph using the CipherCore runtime, there will be no information leakage as desired.
//!
//! Note that the runtime is *not* included in this repository, but its trial version available upon request: [e-mail us](mailto:ciphercore@ciphermode.tech).
//!
//! Now let us execute the compiled graph locally, for the evaluation purposes.
//! Let us paste the following two 5x5 matrices that comprise input data to the file `inputs.json`:
//! ```json
//! [
//!     {"kind": "array",
//!      "type": "i64",
//!      "value": [[1, 2, 3, 4, 5],
//!                [6, 7, 8, 9, 10],
//!                [11, 12, 13, 14, 15],
//!                [16, 17, 18, 19, 20],
//!                [21, 22, 23, 24, 25]]},
//!     {"kind": "array",
//!      "type": "i64",
//!      "value": [[21, 22, 23, 24, 25],
//!                [26, 27, 28, 29, 30],
//!                [31, 32, 33, 34, 35],
//!                [36, 37, 38, 39, 40],
//!                [41, 42, 43, 44, 45]]}
//! ]
//! ```
//!
//! If we now run the compiled graph on these inputs as follows:
//! ```bash
//! ciphercore_evaluate b.json inputs.json
//! ```
//! we get the correct result:
//! ```json
//! {"kind": "array",
//!  "type": "i64",
//!  "value": [[515, 530, 545, 560, 575],
//!            [1290, 1330, 1370, 1410, 1450],
//!            [2065, 2130, 2195, 2260, 2325],
//!            [2840, 2930, 3020, 3110, 3200],
//!            [3615, 3730, 3845, 3960, 4075]]}
//! ```
//!
//! Instead of the reference evaluator, one can use the binary of a **fast evaluator** that we provide as a part of the CipherCore Docker image. See [this manual](https://github.com/ciphermodelabs/ciphercore/blob/main/reference/main.md#docker-image) for more details.
//! For the above toy example, the difference in the performance is negligible, but for more "serious" examples, it can be dramatic.
//!
//! This tutorial just scratches the surface what one can accomplish using CipherCore. For more, see the remainder of this document (e.g., [Examples](#examples)) as well as [CipherCore documentation](https://docs.rs/ciphercore-base/latest/ciphercore_base/).
//!
//! # Examples
//!
//! The repository contains several examples of how non-trivial algorithms can be created and executed within CipherCore.
//! These examples are structured in a similar way as the [Quick start](#quick-start) example and include:
//! * a documented Rust code creating a computation graph for a specific task (see the [applications](https://docs.rs/ciphercore-base/0.1.0/ciphercore_base/applications/index.html) module).
//! To understand the logic and core concepts of this code, please consult [Graph creation and management](#graph-creation-and-management).
//! This construction logic is covered by unit tests.
//! * a documented Rust code of a binary (check it out [here](https://github.com/ciphermodelabs/ciphercore/tree/main/ciphercore-base/src/bin)) that creates a context with the aforementioned graph and returns its serialization into JSON.
//! This serialization can be later used for converting the graph to its secure computation counterpart, visualization and inspection as was shown in [Quick start](#quick-start).
//! * two scripts `build_graph.sh` and `run.sh` in [`example_scripts`](https://github.com/ciphermodelabs/ciphercore/tree/main/ciphercore-base/example_scripts)
//!    * `build_graph.sh` creates a computation graph of a secure protocol for a specific task and saves its JSON-serializes it in `mpc_graph.json`.
//!    * `run.sh` takes the graph serialization and runs it on inputs provided in `inputs.json` as in [Quick start](#quick-start).
//!
//! The following examples are provided:
//! * matrix multiplication,
//! * Millionaires' problem,
//! * minimum of an array,
//! * sort using [Radix Sort MPC protocol](https://eprint.iacr.org/2019/695.pdf),
//!
//! ## Matrix multiplication
//!
//! Given two matrices in the form of 2-dimensional arrays, their product is computed.
//! The serialization binary generates the following simple graph, as matrix multiplication is a built-in operation of CipherCore.
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/matmul.svg" alt="Multiplication Graph" width="30%"/>
//! </p>
//!
//! ## Millionaires' problem
//!
//! Two millionaires want to find out who is richer without revealing their wealth.
//! This is [a classic SMPC problem](https://en.wikipedia.org/wiki/Yao%27s_Millionaires%27_problem).
//! The serialization binary generates the following simple graph, as the greater-than operation is a built-in custom operation of CipherCore.
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/millionaires.svg" alt="Millionaires' Problem Graph" width="30%"/>
//! </p>
//!
//! ## Minimum of an array
//!
//! Given an array of unsigned integers, their minimum is computed.
//! The serialization binary generates the following graph corresponding to the tournament method.
//! Note that each `Min` operation is performed elementwise on arrays of 32-bit elements.
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/minimum.svg" alt="Minimum Graph" width="30%"/>
//! </p>
//!
//! ## Sort
//!
//! Given an array of integers, this example sorts them in an ascending order.
//! The serialization binary generates the following graph corresponding to [the Radix Sort MPC protocol](https://eprint.iacr.org/2019/695.pdf).
//!
//! # Graph creation and management
//!
//! The main object of CipherCore is a computation [*graph*](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html).
//! You can think of a graph as an algorithm description where every instruction corresponds to a [*node*](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Node.html).
//! Nodes correspond to operations that can change data, form new data (e.g. [constant nodes](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.constant)) or provide input data (i.e, [input nodes](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.input)).
//!
//! All the computation graphs should exist in a [*context*](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Context.html), which is a special object containing auxiliary information about graphs and nodes. A context can be created by the following function:
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! This context is empty.
//! Let's add a new graph to it:
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! This fresh graph doesn't contain any nodes.
//! Thus, the corresponding algorithm does nothing.
//! Let's implement a simple algorithm, or graph, that adds two 32-bit signed integers.
//!
//! First, define input types of the graph.
//! There are only two input integers of the same type, which is defined below.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! Here, we create a type containing only one integer (i.e., a [*scalar*](https://docs.rs/ciphercore-base/latest/ciphercore_base/data_types/enum.Type.html#variant.Scalar)) of scalar type [INT32](https://docs.rs/ciphercore-base/latest/ciphercore_base/data_types/constant.INT32.html).
//! Similarly, one can create arrays, vectors, tuples and named tuples; see the documentation on [data types](https://docs.rs/ciphercore-base/latest/ciphercore_base/data_types/index.html) for more details.
//!
//! Now, we can add two input nodes to the graph corresponding to two input integers.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! let i1 = g.input(t.clone()).unwrap();
//! let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! Our toy algorithm contains only one instruction, namely "add two input integers".
//! This instruction corresponds to an addition node that can be attached to the graph as follows.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! Note that you can describe various operations via nodes, e.g. arithmetic operations, permutation of arrays, extraction of subarrays, composition of values into vectors or tuples, iteration etc.
//! See [Graph](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html) for more details.
//!
//! Any algorithm should have an output.
//! In the graph language, it means that any graph should have an output node.
//! Let's promote the above addition node to the output node of the graph.
//! Note that the output node can be set only once.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! Now the addition algorithm is fully described as a graph.
//! Now, we should tell CipherCore that the graph is ready by finalizing it.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! After this command the graph can't be changed.
//!
//! CipherCore can evaluate only finalized graphs in a finalized context.
//! To finalize a context, one should set its main graph using the below command.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! ```
//!
//! Similarly to graphs, a context is finalized by the [`finalize`](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Context.html#method.finalize) function; contexts can't be changed after finalization.
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! c.finalize().unwrap();
//! ```
//!
//! The above text gives a glimpse of how computation graphs in CipherCore can be created.
//! For a comprehensive description of the respective API, see [the documentation of CipherCore](https://docs.rs/ciphercore-base/latest/ciphercore_base/index.html).
//!
//! Contexts and graphs can be serialized and deserialized using [serde](https://serde.rs/). Here is how you can serialize a context `c` into JSON:
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # use serde::{Deserialize, Serialize};
//! # let c = create_context().unwrap();
//! # let g = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let i1 = g.input(t.clone()).unwrap();
//! # let i2 = g.input(t).unwrap();
//! # let a = g.add(i1, i2).unwrap(); // you can also write i1.add(i2).unwrap()
//! # g.set_output_node(a).unwrap(); // you can also write a.set_as_output().unwrap()
//! # g.finalize().unwrap();
//! # c.set_main_graph(g).unwrap(); //you can also write g.set_as_main().unwrap()
//! # c.finalize().unwrap();
//! println!("{}", serde_json::to_string(&c).unwrap());
//! ```
//!
//! The resulting graph has the following structure
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/manual_graph.svg" alt="Manual Graph" width="30%"/>
//! </p>
//!
//! ## Overview of CipherCore operations
//!
//! Computation graphs consist of nodes that represent operations.
//! CipherCore operations can be attached to the graph calling a [Graph method](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html).
//! For example,  
//!
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let graph = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let arg1 = graph.input(t.clone()).unwrap();
//! # let arg2 = graph.input(t).unwrap();
//! graph.add(arg1, arg2).unwrap();
//! ```
//!
//! Some operations can be called as a [Node method](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Node.html).
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{INT32, scalar_type};
//! # let c = create_context().unwrap();
//! # let graph = c.create_graph().unwrap();
//! # let t = scalar_type(INT32);
//! # let arg1 = graph.input(t.clone()).unwrap();
//! # let arg2 = graph.input(t).unwrap();
//! arg1.add(arg2).unwrap();
//! ```
//!
//! ### Data types
//!
//! See [documentation](https://docs.rs/ciphercore-base/latest/ciphercore_base/data_types/index.html).
//!
//! Each node in a CipherCore graph has its associated type. Types can be:
//! * **Scalars** A scalar can be a bit or a (signed or unsigned) 8-, 16-, 32- or 64-bit integer.
//! * **(Multi-dimensional) arrays** An array is given by its *shape* and a *scalar entry type*.
//! * **Tuples** A tuple is a fixed-sized sequence of values of potentially different types.
//! * **Named tuples** A named tuple is the same as a tuple except that sequence elements can be addressed by its *names*.
//! * **Vectors** A vector is a sequence of entries of the same type. Unlike arrays, the elements of vectors don't have to be scalars.
//!
//! ### Basic operations
//!
//! CipherCore provides a variety of built-in basic operations that include
//! * [input](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.input),
//! * arithmetic operations (that can operate on the whole arrays at once):
//!    * [addition](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.add),
//!    * [subtraction](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.subtract),
//!    * [multiplication](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.multiply),
//!    * [mixed multiplication of integers and bits](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.mixed_multiply),
//!    * [dot product](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.dot),
//!    * [matrix multiplication](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.matmul),
//!    * [summation of array entries](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.sum),
//!    * [truncation](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.truncate),
//! * [constants](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.constant),
//! * conversion between the binary and arithmetic representations of integers ([a2b](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.a2b), [b2a](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.b2a)),
//! * conversion between vectors and arrays ([array_to_vector](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.array_to_vector) or [vector_to_array](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.vector_to_array)),
//! * composing values into [vectors](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.create_vector), [tuples](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.create_tuple) or [named tuples](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.create_named_tuple),
//! * extracting sub-arrays ([get](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.get), [get_slice](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.get_slice)), vector elements ([vector_get](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.vector_get)) or tuple elements ([tuple_get](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.tuple_get), [named_tuple_get](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.named_tuple_get)),
//! * [permutation](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.permute_axes) of arrays,
//! * [sort](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.sort) of arrays by the key,
//! * [repetition of values](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.repeat),
//! * [reshaping](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.reshape) values to other compatible types,
//! * [joining arrays](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.stack),
//! * [zipping vectors](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.zip),
//! * [calling](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.call) another graph with inputs contained in given nodes,
//! * [iteration](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.iterate).
//!
//! ### Custom operations
//!
//! In addition, CipherCore provides [a custom operation](https://docs.rs/ciphercore-base/latest/ciphercore_base/custom_ops/struct.CustomOperation.html) interface that calls a pre-defined computation graph created for a specific task.
//! Users can create their own custom operations from basic functions by implementing a struct satisfying the [CustomOperationBody](https://docs.rs/ciphercore-base/latest/ciphercore_base/custom_ops/trait.CustomOperationBody.html) trait.
//! The computation graph associated with a custom operation is defined within the [instantiate](https://docs.rs/ciphercore-base/latest/ciphercore_base/custom_ops/trait.CustomOperationBody.html#tymethod.instantiate) method.
//! Note that different computation graphs can be created depending on input types and the number of inputs.
//! Thus, a custom operation is a tool to create [a polymorphic function](https://en.wikipedia.org/wiki/Polymorphism_(computer_science)).
//!
//! To attach a custom operation to the computation graph, use the [custom_op](https://docs.rs/ciphercore-base/latest/ciphercore_base/graphs/struct.Graph.html#method.custom_op) method as follows.
//! ```no_run
//! # use ciphercore_base::graphs::create_context;
//! # use ciphercore_base::data_types::{BIT, array_type};
//! # use ciphercore_base::ops::min_max::Min;
//! # use ciphercore_base::custom_ops::CustomOperation;
//! # let c = create_context().unwrap();
//! # let graph = c.create_graph().unwrap();
//! # let t = array_type(vec![32], BIT);
//! # let arg1 = graph.input(t.clone()).unwrap();
//! # let arg2 = graph.input(t).unwrap();
//! graph.custom_op(CustomOperation::new(Min {signed_comparison: true}), vec![arg1,arg2]).unwrap();
//! ```
//!
//! The following custom operations are already implemented within CipherCore:
//! * [bitwise NOT](https://docs.rs/ciphercore-base/latest/ciphercore_base/custom_ops/struct.Not.html),
//! * [bitwise OR](https://docs.rs/ciphercore-base/latest/ciphercore_base/custom_ops/struct.Or.html),
//! * [the binary adder](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/adder/struct.BinaryAdd.html),
//! * [clipping](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/clip/struct.Clip2K.html),
//! * comparison functions:
//!    * [equal](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.Equal.html),
//!    * [not-equal](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.NotEqual.html),
//!    * [greater-than](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.GreaterThan.html),
//!    * [greater-than-equal-to](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.GreaterThanEqualTo.html),
//!    * [less-than](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.LessThan.html),
//!    * [less-than-equal-to](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/comparisons/struct.LessThanEqualTo.html),
//!    * [maximum](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/min_max/struct.Max.html),
//!    * [minimum](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/min_max/struct.Min.html),
//! * [multiplexer](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/multiplexer/struct.Mux.html),
//! * [multiplicative inverse](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/newton_inversion/struct.NewtonInversion.html),
//! * [inverse square root](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/inverse_sqrt/struct.InverseSqrt.html),
//! * [sorting by integer key](https://docs.rs/ciphercore-base/latest/ciphercore_base/ops/integer_key_sort/struct.SortByIntegerKey.html).
//!
//! # CLI Tools
//!
//! ## Compiler
//!
//! To compile a computation graph to a computation graph of a secure protocol between three parties one can use the CipherCore compiler `ciphercore_compile`.
//!
//! Under the hood, the compilation passes through the following stages:
//! 1. All custom operations of the input graph are instantiated, i.e., they are replaced by the `Call` operations of the graphs that describe the logic of these operations.
//! 2. All `Call` and `Iterate` operations are inlined, i.e., they are replaced by equivalent sets of basic operations without calling other computation graphs.
//! 3. The resulting graph is optimized by removing unnecessary and repetitive operations.
//! 4. Operations of the fully instantiated and inlined graph are converted to their SMPC counterparts.
//! At this stage, `Input` nodes are replaced by operations that perform [secret sharing](#secret-sharing) of input values according to the compiler arguments.
//! The output node of the graph is followed by operations performing revealing to authorized parties.
//! 5. Step 1-3 are repeated on the resulting SMPC graph.
//!
//! The resulting graph is typically larger than the original graph as was shown [above](#working-with-the-graph-using-cli-tools).
//! It includes specific cryptographic and networking operations that help protect and communicate [secret shared values](#secret-sharing).
//!
//! To learn about the invocation of compilation binary and its command-line arguments description, you can run:   
//! ```bash
//! ciphercore_compile --help
//! ```
//!
//! It is invoked as follows:
//! ```bash
//! ciphercore_compile <CONTEXT_PATH> <INLINE_MODE> <INPUT_PARTIES> <OUTPUT_PARTIES>
//! ```
//!
//! where:
//! * `<CONTEXT_PATH>`: The path to a context, where the main graph is to be evaluated privately;
//! * `<INLINE_MODE>`: Before we compile a graph, we instantiate all custom operations, inline all `Call` and `Iterate` operations, and finally optimize the resulting graph. CipherCore offers three different mode for inlining: `simple`, `depth-optimized-default`, and `depth-optimized-extreme`. These modes provide different trade-offs between the compute and the number of networking rounds needed to execute the secure protocol: `simple` mode aims to optimize compute ignoring the networking, `depth-optimized-extreme` minimizes networking latency, while `depth-optimized-default` is somewhere in between.
//! * `<INPUT_PARTIES>`: You should provide a comma delimited list of entities which provide each input. If you specify a number x=0,1,2 it means the party x is providing that input. If you specify `public` it means the input value is public. If you specify `secret-shared` it means that input is secret-shared between all parties. For example, `<INPUT_PARTIES> = 2,public,0,secret-shared` means party 2 provides first input, next input is a public value, the third input is provided by party 0, and the last input is secret-shared among all parties. Check [Secret sharing](#secret-sharing) for technical details.
//! * `<OUTPUT_PARTIES>`: You should provide a comma delimited list of entities that receives the output. Please note that duplicate entries are not allowed in the list. Possible values for `<OUTPUT_PARTIES>` are as follows:
//!    1. `secret-shared`: No party receives the output, it stays in the secret-shared form.
//!    2. `public`: All parties receive the output.
//!    3. A comma delimited list of distinct party numbers: listed parties and only them receive the output.
//!
//! For instance:
//! ```bash
//! ciphercore_compile a.json simple 0,1 2 > b.json
//! ```
//!
//! compiles the graph `a.json` using simple inlining (optimizes for compute rather than network rounds) assuming the first input is provided by party 0, the second input is provided by party 1, and the output is going to be revealed to party 2.
//!
//! ## Evaluator
//!
//! One can run a computation graph (compiled or not) on a given data locally via a reference evaluator, using a binary `ciphercore_evaluate`.
//! In order to use the fast evaluator, please use the binary `ciphercore_evaluate_fast` from within the CipherCore [Docker image](https://github.com/ciphermodelabs/ciphercore/blob/main/reference/main.md#docker-image), which is fully-compatible with `ciphercore_evaluate`.
//! This is a good way to test the functionality as well as -- if we use the fast evaluator -- get a decent idea about the end-to-end performance of the actual protocol when executed within the CipherCore runtime (modulo networking interactions).
//! Either evaluator takes two mandatory parameters: path to a serialized context which main graph we'd like to evaluate and a file with inputs given in the JSON format.
//!
//! ### Secret-shared input
//!
//! If an input to a compiled graph is given in a [secret-shared format](#secret-sharing), you can optionally provide a vanilla plaintext input, and it will be secret-shared automatically.
//!
//! ### Input format
//!
//! Inputs and outputs are given in a human-readable JSON format. For example:
//!
//! ```json
//! [
//!     {"kind": "scalar", "type": "i32", "value": 123456},
//!     {"kind": "array", "type": "bit", "value": [[0, 1, 1, 0], [1, 0, 0, 1], [1, 0, 0, 1], [0, 1, 1, 0]]},
//!     {"kind": "tuple", "value": [{"kind": "scalar", "type": "i32", "value": 123456}, {"kind": "tuple", "value": []}]},
//!     {"kind": "vector", "value": [{"kind": "scalar", "type": "i32", "value": 123456}, {"kind": "scalar", "type": "i32", "value": 654321}]}
//! ]
//! ```
//!
//! You can learn more by checking out the [provided examples](#examples).
//!
//! ## Visualization
//!
//! The visualization tool, namely `ciphercore_visualize_context`, generates a set of instructions for GraphViz to draw all the graphs and their associated nodes from the given `Context` input.
//! To use it, you need to [install](https://graphviz.org/download/) Graphviz.
//!
//! For instance, if we create the following context:
//!
//! ```no_run
//! use ciphercore_base::data_types::{array_type, UINT64};
//! use ciphercore_base::errors::Result;
//! use ciphercore_base::graphs::create_context;
//!
//! fn main() {
//!     || -> Result<()> {
//!         let c = create_context()?;
//!         let mul = {
//!             let g = c.create_graph()?;
//!             let i0 = g.input(array_type(vec![2, 2], UINT64))?;
//!             i0.set_name("MultIp0")?;
//!             let i1 = g.input(array_type(vec![2, 2, 2], UINT64))?;
//!             i1.set_name("MultIp1")?;
//!             let op_mul = g.multiply(i0, i1)?;
//!             op_mul.set_name("Product")?;
//!             g.set_output_node(op_mul)?;
//!             g.finalize()?;
//!             g
//!         };
//!         let sum_g = c.create_graph()?;
//!         let i0 = sum_g.input(array_type(vec![2], UINT64))?;
//!         i0.set_name("Input a")?;
//!         let i1 = sum_g.input(array_type(vec![2, 2], UINT64))?;
//!         i1.set_name("Input b")?;
//!         let i2 = sum_g.input(array_type(vec![2, 2, 2], UINT64))?;
//!         i2.set_name("Input c")?;
//!         let prod = sum_g.call(mul, vec![i1, i2])?;
//!         let op = sum_g.add(i0, prod)?;
//!         op.set_name("Output")?;
//!         sum_g.set_output_node(op)?;
//!         sum_g.finalize()?;
//!         c.set_main_graph(sum_g)?;
//!         c.finalize()?;
//!         println!("{}", serde_json::to_string(&c)?);
//!         Ok(())
//!     }()
//!     .unwrap();
//! }
//! ```
//!
//! save the output to file `context.json`, and visualize it as follows:
//!
//! ```bash
//! ciphercore_visualize_context context.json | dot -Tsvg -o vis.svg
//! ```
//!
//! we get:
//!
//! <p align = "center">
//!     <img src="https://raw.githubusercontent.com/ciphermodelabs/ciphercore/main/reference/images/arr_mul.svg" alt="Array Multiplication Graph" width="60%"/>
//! </p>
//!
//! ## Inspection
//!
//! Using graph inspection, you can get insightful statistics about a computation graph.
//! These statistics include names and types of all of the input nodes, name and type of the output node, number of network rounds required to evaluate the graph, number of arithmetic operations required to evaluate the graph, and number of times each type of node occurring in the graph.
//!
//! To learn about the invocation of graph inspection binary and its command-line arguments description, you can run:   
//!
//! ```bash
//! ciphercore_inspect --help
//! ```
//!
//! You can inspect both compiled and uncompiled graphs. For example, for a compiled graph stored in `b.json` you can simply run inspect by:
//!
//! ```bash
//! ciphercore_inspect b.json
//! ```
//!
//! and get a result like:
//!
//! ```bash
//! Calculating stats...
//! -------Stats--------
//! Inputs:
//!     1. Name:unnamed
//!     Type:i64[5, 5]
//!     2. Name:unnamed
//!     Type:i64[5, 5]
//! Output:
//!     Name:unnamed
//!     Type:i64[5, 5]
//! Network rounds: 4
//! Network traffic: 2.00KB
//! Total number of integer arithmetic operations:   2.84K Ops
//!     Total number of 1-bit arithmetic operations:   384 Ops
//!     Total number of 8-bit arithmetic operations:   0 Ops
//!     Total number of 16-bit arithmetic operations:  0 Ops
//!     Total number of 32-bit arithmetic operations:  0 Ops
//!     Total number of 64-bit arithmetic operations:  2.45K Ops
//! Total operations: 55
//! Operations:
//!     NOP           13
//!     Add           13
//!     PRF           9
//!     Subtract      9
//!     Matmul        6
//!     Random        3
//!     Input         2
//! ```
//!
//! For uncompiled graphs, you have the option to first prepare the graph for inspection.
//! In preparation phase, we instantiate all custom operations, inline all `Call` and `Iterate` operations, and finally optimize the resulting graph.
//! CipherCore offers three different mode for inlining: `simple`, `depth-optimized-default`, and `depth-optimized-extreme`.
//! You can chose which inlining mode should be used for preparing the input graph.
//! If you do not chose any inlining mode, the `simple` mode will be used as a default.
//! For example, for an uncompiled graph stored in `a.json` you can run inspect by:
//!
//! ```bash
//! ciphercore_inspect a.json prepare depth-optimized-default
//! ```
//!
//! and get a result as follows:
//!
//! ```bash
//! Instantiating...
//! Inlining...
//! Optimizing...
//! Calculating stats...
//! -------Stats--------
//! Inputs:
//!     1. Name:unnamed
//!     Type:i64[5, 5]
//!     2. Name:unnamed
//!     Type:i64[5, 5]
//! Output:
//!     Name:unnamed
//!     Type:i64[5, 5]
//! Network rounds: 0
//! Network traffic: 0B
//! Total number of integer arithmetic operations:   125 Ops
//!     Total number of 1-bit arithmetic operations:   0 Ops
//!     Total number of 8-bit arithmetic operations:   0 Ops
//!     Total number of 16-bit arithmetic operations:  0 Ops
//!     Total number of 32-bit arithmetic operations:  0 Ops
//!     Total number of 64-bit arithmetic operations:  125 Ops
//! Total operations: 3
//! Operations:
//!     Input         2
//!     Matmul        1
//! ```
#![allow(clippy::needless_doctest_main)]

#[macro_use]
pub mod errors;
pub mod applications;
#[doc(hidden)]
pub mod broadcast;
#[doc(hidden)]
pub mod bytes;
mod constants;
pub mod custom_ops;
pub mod data_types;
pub mod data_values;
#[doc(hidden)]
pub mod evaluators;
pub mod graphs;
#[doc(hidden)]
pub mod inline;
#[doc(hidden)]
pub mod join_utils;
#[doc(hidden)]
pub mod mpc;
pub mod ops;
#[doc(hidden)]
pub mod optimizer;
#[doc(hidden)]
pub mod random;
#[doc(hidden)]
pub mod slices;
#[doc(hidden)]
pub mod type_inference;
pub mod typed_value;
#[doc(hidden)]
pub mod typed_value_operations;
#[doc(hidden)]
pub mod typed_value_secret_shared;
#[doc(hidden)]
mod typed_value_serialization;
#[doc(hidden)]
pub mod version;

#[cfg(test)]
#[macro_use]
extern crate maplit;