Function proj

Source

pub fn proj(lon: f64, lat: f64) -> (f64, f64)

Expand description

Performs the HEALPix projection: (x, y) = proj(lon, lat).
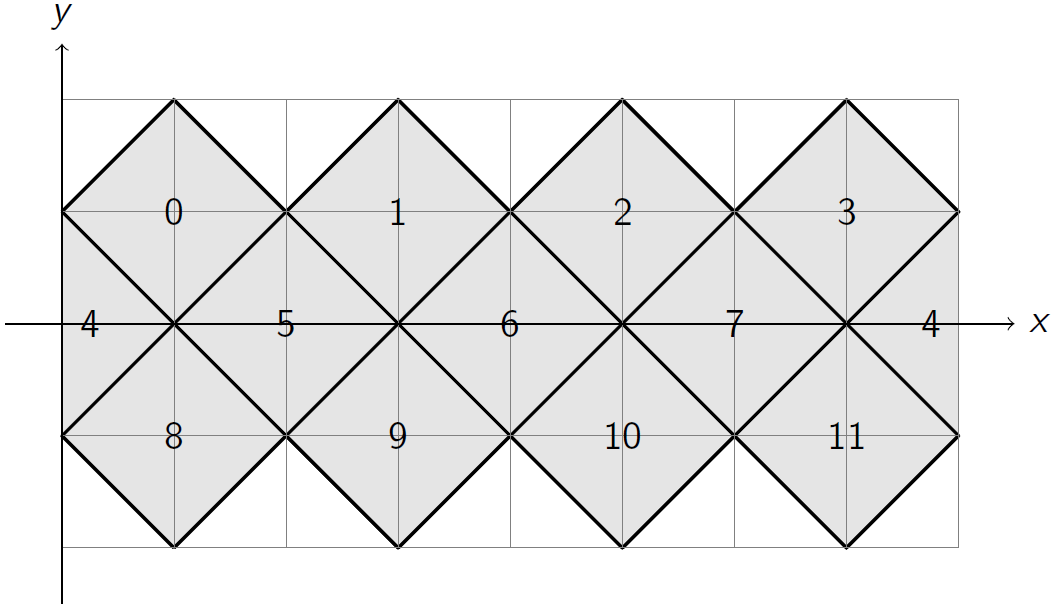
The chosen scale is such that: base cell vertices and center coordinates are integers; the distance from a cell center to its vertices equals one.
This projection is multi-purpose in the sense that if lon is in [-pi, pi], then x is in [-4, 4] and if lon is in [0, 2pi], then x is in [0, 8].
It means that a same position on the sphere can lead to different positions in the projected Euclidean plane.

Simplified projection formulae are:

Equatorial region

\boxed{
  \left\{
    \begin{array}{lcl}
      X & = & \alpha \times \frac{4}{\pi} \\
      Y & = & \sin(\delta) \times \frac{3}{2}
    \end{array}
  \right.
}
\Rightarrow
\left\{
  \begin{array}{lcl}
    \alpha \in [0, 2\pi] & \leadsto &  X \in [0, 8] \\
    \sin\delta \in [-\frac{2}{3}, \frac{2}{3}] & \leadsto & Y \in [-1, 1]
  \end{array}
\right.

Polar caps:

\boxed{
  \left\{
    \begin{array}{lcl}
      t & = & \sqrt{3(1-\sin\delta)} \\
      X & = & (\alpha\frac{4}{\pi} - 1)t+1 \\
      Y & = & 2 - t
    \end{array}
  \right.
}
\Rightarrow
\left\{
  \begin{array}{l}
    \alpha \in [0, \frac{\pi}{2}] \\
    \sin\delta \in ]\frac{2}{3}, 1]
  \end{array}
\right.
\leadsto
\begin{array}{l}
   t \in [0, 1[  \\
   X \in ]0, 2[ \\
   Y \in ]1, 2]
\end{array}

It is the responsibility of the caller to homogenize the result according to its needs. Proj

§Inputs

lon longitude in radians, support positive and negative reasonably large values (naive approach, no Cody-Waite nor Payne Hanek range reduction).
lat latitude in radians, must be in [-pi/2, pi/2]

§Output

(x, y) the projected planar Euclidean coordinates of the point of given coordinates (lon, lat) on the unit sphere
- lon ≤ 0 => x in [-8, 0]
- lon ≥ 0 => x in [0, 8]
- y in [-2, 2]

§Panics

If lat not in [-pi/2, pi/2], this method panics.

§Examples

To obtain the WCS projection (see Calabretta2007), you can write:

use cdshealpix::proj;
use std::f64::consts::{PI, FRAC_PI_2, FRAC_PI_4};

let lon = 25.1f64;
let lat = 46.7f64;

let (mut x, mut y) = proj(lon.to_radians(), lat.to_radians());
if x > 4f64 {
  x -= 8f64;
}
x *= FRAC_PI_4;
y *= FRAC_PI_4;

assert!(-PI <= x && x <= PI);
assert!(-FRAC_PI_2 <= y && y <= FRAC_PI_2);

Other test example:

use cdshealpix::{TRANSITION_LATITUDE, proj};
use std::f64::consts::{FRAC_PI_2, FRAC_PI_4};

let (x, y) = proj(0.0, 0.0);
assert_eq!(0f64, x);
assert_eq!(0f64, y);

assert_eq!((0.0, 1.0), proj(0.0 * FRAC_PI_2, TRANSITION_LATITUDE));

fn dist(p1: (f64, f64), p2: (f64, f64)) -> f64 {
    f64::sqrt((p2.0 - p1.0) * (p2.0 - p1.0) + (p2.1 - p1.1) * (p2.1 - p1.1))
}
assert!(dist((0.0, 0.0), proj(0.0 * FRAC_PI_2, 0.0)) < 1e-15);
assert!(dist((0.0, 1.0), proj(0.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((1.0, 2.0), proj(0.0 * FRAC_PI_2 + FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((2.0, 1.0), proj(1.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((3.0, 2.0), proj(1.0 * FRAC_PI_2 + FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((4.0, 1.0), proj(2.0 * FRAC_PI_2 , TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((5.0, 2.0), proj(2.0 * FRAC_PI_2 + FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((6.0, 1.0), proj(3.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((7.0, 2.0), proj(3.0 * FRAC_PI_2 + FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((0.0, 1.0), proj(4.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((0.0, 0.0), proj(4.0 * FRAC_PI_2, 0.0)) < 1e-15);
assert!(dist((0.0, -1.0), proj(0.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((1.0, -2.0), proj(0.0 * FRAC_PI_2 + FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((2.0, -1.0), proj(1.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((3.0, -2.0), proj(1.0 * FRAC_PI_2 + FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((4.0, -1.0), proj(2.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((5.0, -2.0), proj(2.0 * FRAC_PI_2 + FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((6.0, -1.0), proj(3.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((7.0, -2.0), proj(3.0 * FRAC_PI_2 + FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((0.0, -1.0), proj(4.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);

assert!(dist((-0.0, 0.0), proj(-0.0 * FRAC_PI_2, 0.0)) < 1e-15);
assert!(dist((-0.0, 1.0), proj(-0.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-1.0, 2.0), proj(-0.0 * FRAC_PI_2 - FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((-2.0, 1.0), proj(-1.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-3.0, 2.0), proj(-1.0 * FRAC_PI_2 - FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((-4.0, 1.0), proj(-2.0 * FRAC_PI_2 , TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-5.0, 2.0), proj(-2.0 * FRAC_PI_2 - FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((-6.0, 1.0), proj(-3.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-7.0, 2.0), proj(-3.0 * FRAC_PI_2 - FRAC_PI_4, FRAC_PI_2)) < 1e-15);
assert!(dist((-0.0, 1.0), proj(-4.0 * FRAC_PI_2, TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-0.0, 0.0), proj(-4.0 * FRAC_PI_2, 0.0)) < 1e-15);
assert!(dist((-0.0, -1.0), proj(-0.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-1.0, -2.0), proj(-0.0 * FRAC_PI_2 - FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((-2.0, -1.0), proj(-1.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-3.0, -2.0), proj(-1.0 * FRAC_PI_2 - FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((-4.0, -1.0), proj(-2.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-5.0, -2.0), proj(-2.0 * FRAC_PI_2 - FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((-6.0, -1.0), proj(-3.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);
assert!(dist((-7.0, -2.0), proj(-3.0 * FRAC_PI_2 - FRAC_PI_4, -FRAC_PI_2)) < 1e-15);
assert!(dist((-0.0, -1.0), proj(-4.0 * FRAC_PI_2, -TRANSITION_LATITUDE)) < 1e-15);

Function projCopy item path

§Inputs

§Output

§Panics

§Examples

Function proj