Module eta_reduce 

Carries out simple eta-reduction, to reduce the amount of rewrites at runtime.

Eta-equivalence

In interaction combinators, there are some nets that are equivalent and have no observable difference

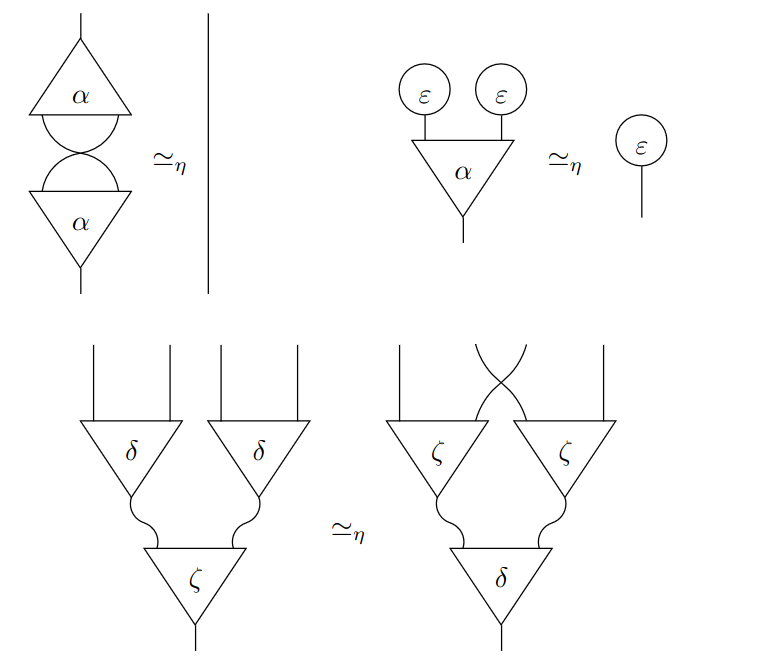
This module implements the eta-equivalence rule at the top-left of the image above

    /|-, ,-|\     eta_reduce
---| |  X  | |-- ~~~~~~~~~~~~> -------------
    \|-' '-|/

In hvm-core’s AST representation, this reduction looks like this

{lab x y} ... {lab x y} ~~~~~~~~> x ..... x

Essentially, both occurrences of the same constructor are replaced by a variable.

The algorithm

The code uses a two-pass O(n) algorithm, where n is the amount of nodes in the AST

In the first pass, a node-list is built out of an ordered traversal of the AST. Crucially, the node list stores variable offsets instead of the variable’s names Since the AST’s order is consistent, the ordering of nodes in the node list can be reproduced with a traversal.

This means that each occurrence of a variable is encoded with the offset in the node-list to the other occurrence of the variable.

For example, if we start with the net: [(x y) (x y)]

The resulting node list will look like this:

[Ctr(1), Ctr(0), Var(3), Var(3), Ctr(0), Var(-3), Var(-3)]

The second pass uses the node list to find repeated constructors. If a constructor’s children are both variables with the same offset, then we lookup that offset relative to the constructor. If it is equal to the first constructor, it means both of them are equal and they can be replaced with a variable.

The pass also reduces subnets such as (* *) -> *

Functions

eta_reduce_hvm_net

Carries out simple eta-reduction