[−][src]Crate impulse_response
Impulse Response Integration Method
A tool for simulating dynamical systems.
This method works by measuring the impulse response of the system. If the system is linear and time-invariant then the impulse response completely describes the system. The exact state of the system can be computed by convolving the initial state of the system with the impulse response. This method uses these facts to solve integration problems with efficient matrix-vector multiplications.
Details
Users specify their system with both:
-
A state vector, which completely describes the system at an instant in time.
-
The derivative of the state, as a function of the current state.
The users system is assumed to be linear and time-invariant.
This method uses the impulse response to advance the state of the system in
fixed time steps of length time_step. First compute the impulse response in
high fidelity using the Crank-Nicholson method with a variable length time-step.
Sample the response at time_step after the impulse. Measure the impulse
response of every state and store them in a matrix. Then to advance the state of
the integration, multiply that matrix by the state vector.
The impulse response matrix is a square matrix, and so its size is the length of
the state vector squared. Naively, this could cause performance issues for
systems which have a very large state vector. However in most systems with very
large state vectors: most of the states do not interact with each other over the
relatively short time_step at which it measures the impulse response. As a
result, the impulse responses are mostly zeros and the impulse response matrix
can be compressed into a sparse matrix.
The impulse response integration method runs fast, but can consume a significant amount of time and memory at start up to compute and store the impulse responses.
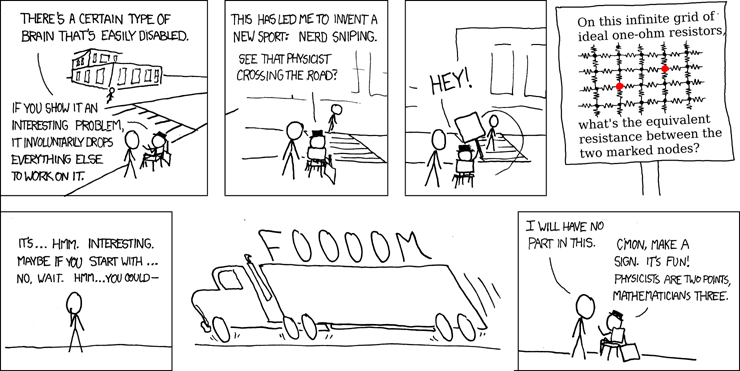
Example: Measuring equivalent resistance
This comic strip poses an interesting problem. The problem does have a known
analytic solution, 4/pi - 1/2, but it can also be approximated using numerical
methods. I demonstrate how to do this using the impulse response library.
Numerical Solution
-
First alter the size of the grid of resistors, from an infinite grid to a very large grid. Otherwise it would not be possible to compute! Because of this change the resulting approximation will overestimate the true value. In the limit, as the size of the grid approaches infinity, this overestimation error approaches zero.
-
Attach a capacitor to every node in the grid. This simulates the parasitic capacitance which exists in all wires. Capacitance needs to be included in the model in order to simulate the flow of electric charge.
-
Connect a voltage source across the two marked nodes, and measure how much current passes through the voltage source. Then compute the equivalent resistance using the formula:
V = I R. Since the system contains capacitors, it will take time for the current to reach a steady state. Measuring the steady state current entails simulating the system for a considerable amount of time.
Implementation and Results
The source code is an annotated example of how to use this library. Link: impulse_response/examples/nerd_sniping.rs
Result of running the code with a 32x32 grid:
$ time cargo run --example nerd_sniping --release Model Size: 1024 Nodes Equivalent Resistance: 0.8825786612296072 Ohms Exact Answer: 4/PI - 1/2 = 0.7732395447351628 Ohms
Now lets increase the size of the grid to 633x633, and observe that the equivalent resistance is closer to the correct value:
$ cargo run --example nerd_sniping --release Model Size: 400689 Nodes Equivalent Resistance: 0.8416329950362197 Ohms Exact Answer: 4/PI - 1/2 = 0.7732395447351628 Ohms
Runtime: 2 days.
The measurement error is approximately 8%.
More Examples
-
tests/exponential_decay.rs- Smoke test, simulates a system which simply decays exponentially.
-
examples/benchmark.rs- An artificial scenario.
- Demonstrates modifying the system while its running.
-
tests/leaky_cable.rs- Simulates the electricity in a neurons dendrite.
Modules
| sparse | Large sparsely connected systems |