Crate adapton

Expand description

§Adapton for Rust

This Rust implementation embodies the latest implementation Adapton, which offers a foundational, language-based semantics for general-purpose incremental computation.

§Programming model

The documentation below gives many illustrative examples, with pointers into the other Rust documentation.
The engine module gives the core programming interface.

§Resources

§Background

Adapton proposes the demanded computation graph (or DCG), and a demand-driven change propagation algorithm. Further, it proposes first-class names for identifying cached data structures and computations. For a quick overview of the role of names in incremental computing, we give background on incremental computing with names, below.

The following academic papers detail these technical proposals:

DCG, and change propagation: Adapton: Composable, demand-driven incremental computation, PLDI 2014.
Nominal memoization: Incremental computation with names, OOPSLA 2015.
Type and effect structures: The draft Typed Adapton: Refinement types for incremental computation with precise names.

§Why Rust?

Adapton’s first implementations used Python and OCaml; The latest implementation in Rust offers the best performance thus far, since (1) Rust is fast, and (2) traversal-based garbage collection presents performance challenges for incremental computation. By liberating Adapton from traversal-based collection, our empirical results are both predictable and scalable.

§Adapton programming model

Adapton roles: Adapton proposes editor and achivist roles:

The Editor role creates and mutates input, and demands the output of incremental computations in the Archivist role.
The Archivist role consists of Adapton thunks, where each is cached computation that consumes incremental input and produces incremental output.

Examples: The examples below illustrate these roles, in increasing complexity:

Start the DCG engine
Create incremental cells
Observe Arts
Mutate input cells
Demand-driven change propagation and switching
Memoization
Create thunks
Use force_map for more precise dependencies
Nominal memoization
Nominal cycles
Nominal firewalls

Programming primitives: The following list of primitives covers the core features of the Adapton engine. Each primitive below is meaningful in each of the two, editor and archivist, roles:

Ref cell allocation: Mutable input (editor role), and cached data structures that change across runs (archivist role).
- cell! – Preferred version
- let_cell! – Useful in simple examples
- engine::cell – Engine’s raw interface
Observation and demand: Both editor and archivist role.
- get! – Preferred version
- engine::force – Engine’s raw interface
- engine::force_map – A variant for observations that compose before projections
Thunk Allocation: Both editor and archivist role.
- Thunk allocation, without demand:
  - thunk! – Preferred version
  - let_thunk! – Useful in simple examples
  - engine::thunk – Engine’s raw interface (can be cumbersome)
- Thunk allocation, with demand:
  - memo! – Preferred version
  - let_memo! – Useful in simple examples

§Start the DCG engine

The call init_dcg() below initializes a DCG-based engine, replacing the Naive default engine.

#[macro_use] extern crate adapton;
use adapton::macros::*;
use adapton::engine::*;

fn main() {
    manage::init_dcg();

    // Put example code below here
}

§Create incremental cells

Commonly, the input and intermediate data of Adapton computations consists of named reference cells. A reference cell is one variety of Arts; another are thunks.

§Implicit `cell` names

Behind the scenes, the (editor’s) invocation cell!(123) uses an imperative global counter to choose a unique name to hold the number 123. After each use, it increments this global counter, ensuring that each such number is used at most once.

let c : Art<usize> = cell!( 123 );

assert_eq!( get!(c), 123 );

§Naming strategy: Global counter

Using a global counter to name cells, as above, may be appopriate for the Editor role, but is never appropriate for the Archivist role, since this global counter is too sensitive to global (often-changing) properties, such as an index into the sequence of all allocations, globally.

To replace this global counter, we the Archivist may give names explicitly, as shown in various forms, below.

§Explicitly named `cell`s

§Names via Rust “identifiers”

Sometimes we name a cell using a Rust identifier. We specify this case using the notation [ name ], which specifies that the cell’s name is a string, constructed from the Rust identifer name:

let c : Art<usize> = cell!([c] 123);

assert_eq!(get!(c), 123);

§Optional `Name`s

Most generally, we supply an expression optional_name of type Option<Name> to specify the name for the Art. This Art is created by either cell or put, in the case that optional_name is Some(name) or None, respectively:

let n : Name = name_of_str(stringify!(c));
let c : Art<usize> = cell!([Some(n)]? 123);

assert_eq!(get!(c), 123);

let c = cell!([None]? 123);

assert_eq!(get!(c), 123);

§Observe `Art`s

The macro get! is sugar for engine::force!, with reference introduction operation &:

let c : Art<usize> = cell!(123);

assert_eq!( get!(c), force(&c) );

Since the type Art<T> classifies both cells and thunks, the operations force and get! can be used interchangeably on Art<T>s that arise as cells or thunks.

§Mutate input cells

One may mutate cells explicitly, or implicitly, which is common in Nominal Adapton.

The editor (implicitly or explicitly) mutates cells that hold input and they re-demand the output of the archivist’s computations. During change propagation, the archivist mutates cells with implicit mutation.

Implicit mutation uses nominal allocation: By allocating a cell with the same name, one may overwrite cells with new content:

let n : Name = name_of_str(stringify!(c));
let c : Art<usize> = cell!([Some(n.clone())]? 123);

assert_eq!(get!(c), 123);

// Implicit mutation (re-use cell by name `n`):
let d : Art<usize> = cell!([Some(n)]? 321);

assert_eq!(d, c);
assert_eq!(get!(c), 321);
assert_eq!(get!(d), 321);

No names implies no effects: Using None to allocate cells always **gives distinct cells, with no overwriting:


let c = cell!([None]? 123);
let d = cell!([None]? 321);

assert_eq!(get!(c), 123);
assert_eq!(get!(d), 321);

Explicit mutation, via set: If one wants mutation to be totally explicit, one may use set:

let n : Name = name_of_str(stringify!(c));
let c : Art<usize> = cell!([Some(n)]? 123);

assert_eq!(get!(c), 123);

// Explicit mutation (overwrites cell `c`):
set(&c, 321);

assert_eq!(get!(c), 321);

§Demand-driven change propagation

The example below demonstrates demand-driven change propagation, which is unique to Adapton’s DCG, and its approach to incremental computation. The example DCG below consists of two kinds of nodes:

Cells consist of data that changes over time, including (but not limited to) incremental input.
Thunks consist of computations whose observations and results are cached in the DCG.

The simple example below uses two mutable input cells, num and den, whose values are used by an intermediate subcomputation div that divides the numerator in num by the denominator in den, and a thunk check that first checks whether the denominator is zero (returning zero if so) and if non-zero, returns the value of the division:

// Two mutable inputs, for numerator and denominator of division
let num = cell!(42);
let den = cell!(2);

// In Rust, cloning is explicit:
let den2 = den.clone(); // clone _global reference_ to cell.
let den3 = den.clone(); // clone _global reference_ to cell, again.

// Two subcomputations: The division, and a check thunk with a conditional expression
let div   = thunk![ get!(num) / get!(den) ];
let check = thunk![ if get!(den2) == 0 { None } else { Some(get!(div)) } ];

After allocating num, den and check, the programmer changes den and observes check, inducing the following change propagation behavior. In sum, whether div runs is based on demand from the Editor (of the output of check), and the value of input cell den, via the condition in check:

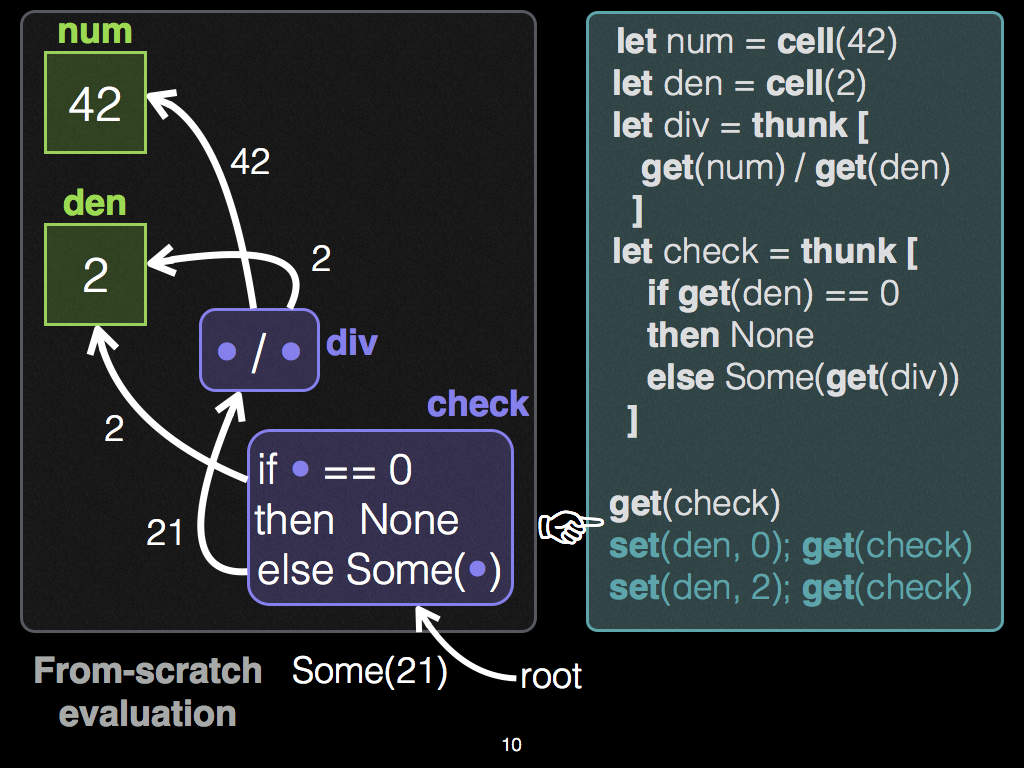
When the thunk check is demanded for first time, Adapton executes the condition, and cell den holds 2, which is non-zero. Hence, the else branch executes get!(div), which demands the output of the division, 21.
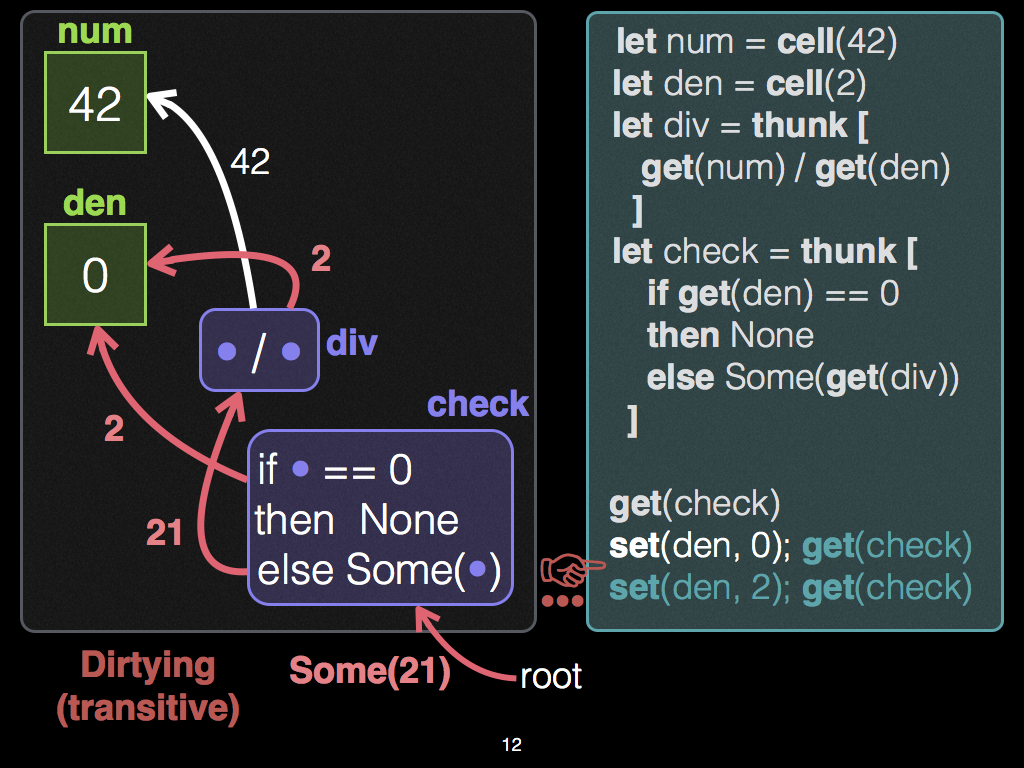
After this first observation of check, the programmer changes cell den to 0, and re-demands the output of thunk check. In response, Adapton’s change propagation algorithm first re-executes the condition (not the division), and the condition branches to the then branch, resulting in None; in particular, it does not re-demand the div node, though this node still exists in the DCG.
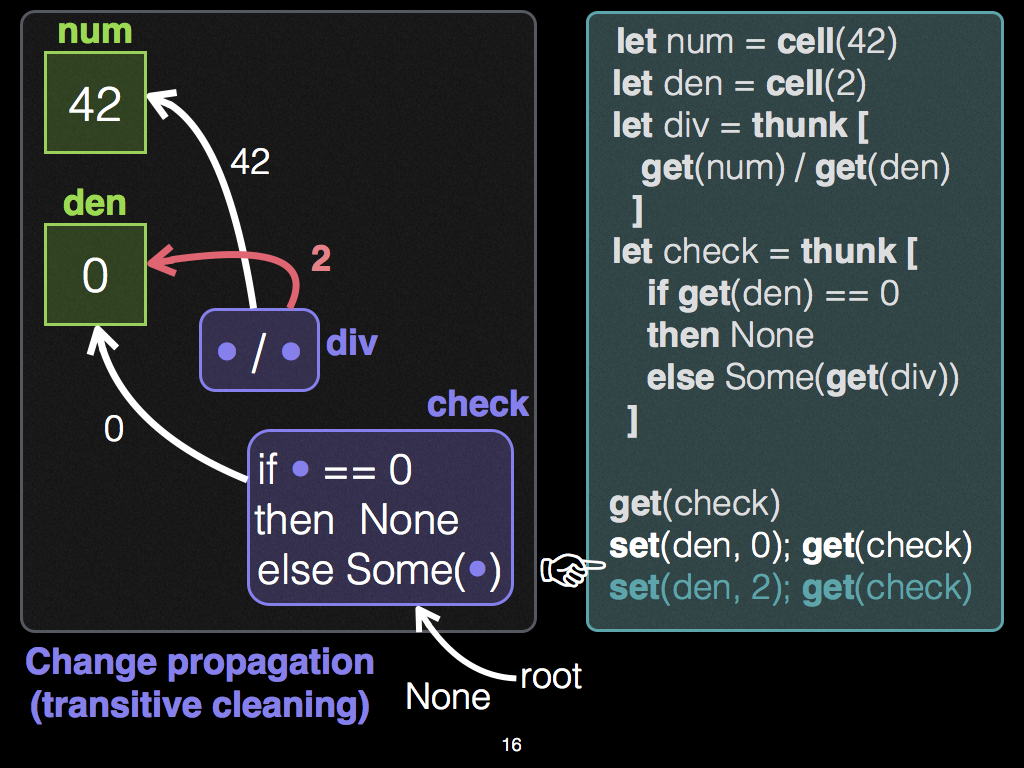
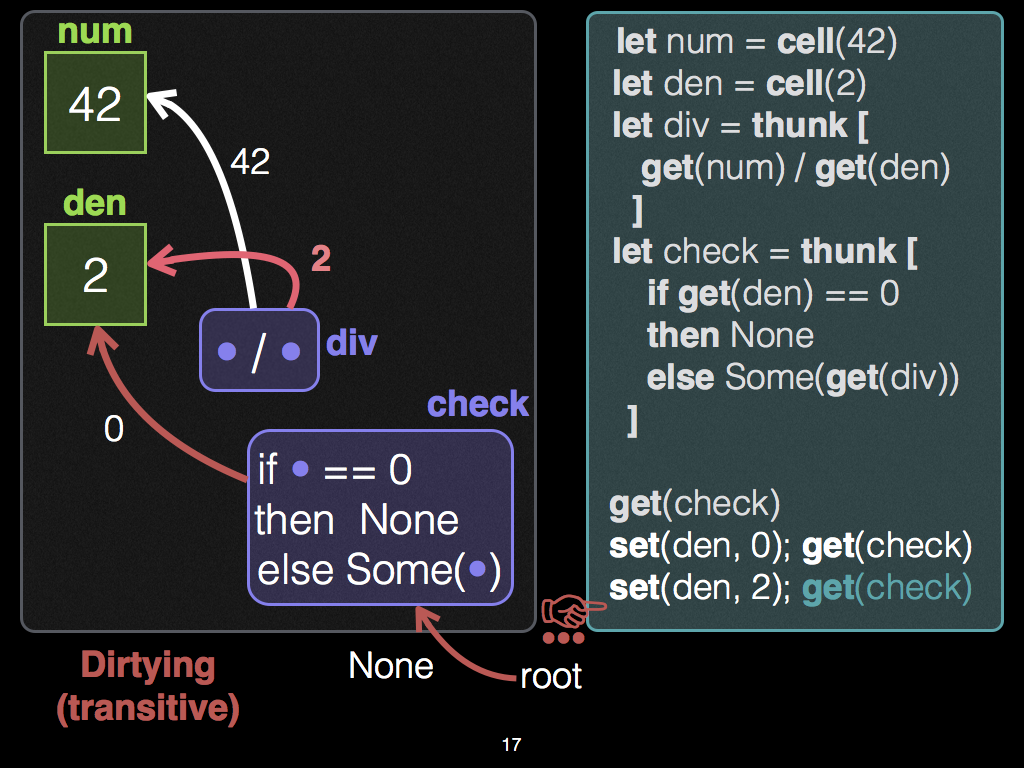
Next, the programmer changes den back to its original value, 2, and re-demands the output of check. In response, change propagation re-executes the condition, which re-demands the output of div. Change propagation attempts to “clean” the div node before re-executing it. To do so, it compares its last observations of num and den to their current values, of 42 and 2, respectively. In so doing, it finds that these earlier observations match the current values. Consequently, it reuses the output of the division (21) without having to re-execute the division.

// Observe output of `check` while we change the input `den`
// Editor Step 1: (Explained in detail, below)
assert_eq!(get!(check), Some(21));

// Editor Step 2: (Explained in detail, below)
set(&den3, 0);
assert_eq!(get!(check), None);

// Editor Step 3: (Explained in detail, below)
set(&den3, 2);
assert_eq!(get!(check), Some(21));  // division is reused

Slides with illustrations of the graph structure and the code side-by-side may help:

Editor Step 1

Slide-10

Editor Steps 2 and 3

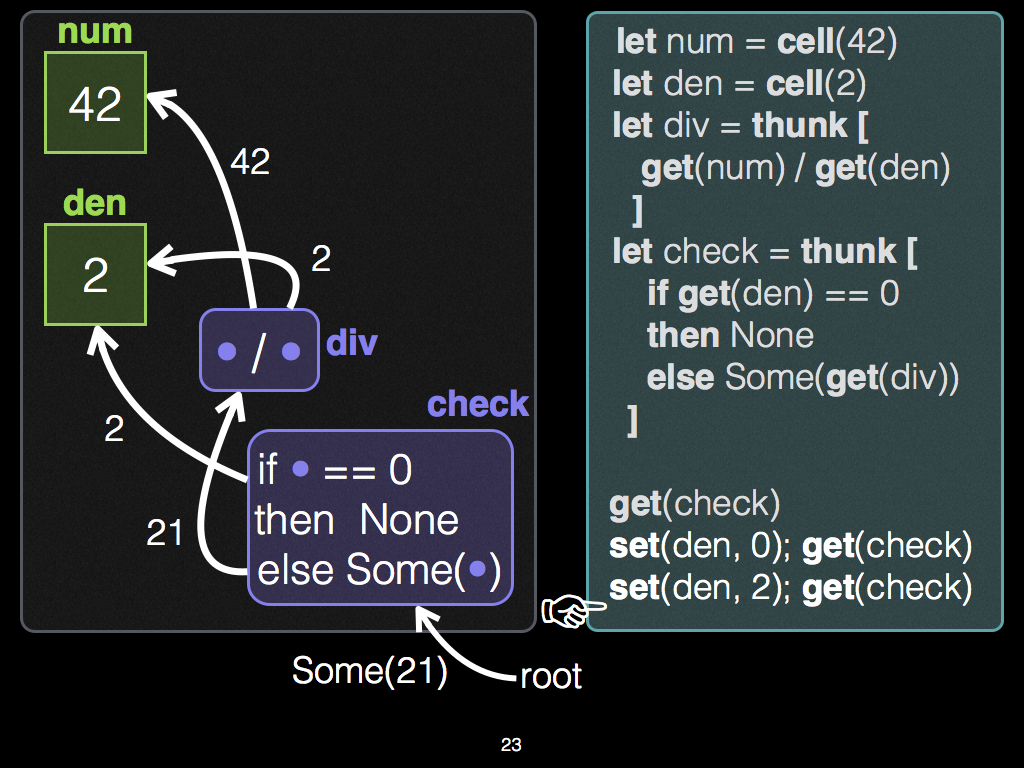
Slide_12 Slide_16 Slide-17 Slide-23

Full-sized slides

In sum, whether div runs is based on demand from the Editor (of check), and the value of input den. The reuse of div illustrates the switching pattern, which is unique to Adapton’s approach to incremental computation.

§Switching

In the academic literature on Adapton, we refer to the three-step pattern of change propagation illustrated above as switching:

Past work on self-adjusting computation does not support the switching pattern directly: Because of its change propagation semantics, it would “forget” the division in step 2, and rerun it from-scratch in step 3.

Furthermore, some other change propagation algorithms base their re-execution schedule on “node height” (of the graph’s topological ordering). These algorithms may also have undesirable behavior. In particular, they may re-execute the division div in step 2, though it is not presently in demand. For an example, see this gist.

§Memoization

Memoization provides a mechanism for caching the results of subcomputations; it is a crtical feature of Adapton’s approach to incremental computation.

In Adapton, each memoization point has three ingredients:

A function expression (of type Fn)
Zero or more arguments. Each argument type must have an implementation for the traits Eq + Clone + Hash + Debug. The traits Eq and Clone are both critical to Adapton’s caching and change propagation engine. The trait Hash is required when Adapton’s naming strategy is structural (e.g., where function names are based on the hashes of their arguments). The trait Debug is useful for debugging, and reflection.
An optional name, which identifies the function call for reuse later.
- When this optional name is None, the memoization point may be treated in one of two ways: either as just an ordinary, uncached function call, or as a cached function call that is identified structurally, by its function pointer and arguments. Adapton permits structural subcomputations via the engine’s structural function.
- When this is Some(name), the memoization point uses name to identify the work performed by the function call, and its result. Critically, in future incremental runs, it is possible for name to associate with different functions and/or argument values.

Each memoization point yields two results:

A thunk articulation, of type Art<Res>, where Res is the result type of the function expression.
A result value of type Res, which is also cached at the articulation.

§Optional name version

The following form is preferred:

memo!( [ optional_name ]? fnexp ; lab1 : arg1, ..., labk : argk )

It accepts an optional name, of type Option<Name>, and an arbitrary function expression fnexp (closure or function pointer). Like the other forms, it requires that the programmer label each argument.

§Example

let (t,z) : (Art<usize>, usize) =
  memo!([Some(name_unit())]?
    |x:usize,y:usize|{ if x > y { x } else { y }};
     x:10,   y:20   );

assert_eq!(z, 20);

More examples of memo! macro

§Create thunks

Thunks consist of suspended computations whose observations, allocations and results are cached in the DCG, when forced. Each thunk has type Art<Res>, where Res is the return type of the thunk’s suspended computation.

Each memoization point is merely a forced thunk. We can also create thunks without demanding them.

The following form is preferred:

thunk!( [ optional_name ]? fnexp ; lab1 : arg1, ..., labk : argk )

It accepts an optional name, of type Option<Name>, and an arbitrary function expression fnexp (closure or function pointer). Like the other forms, it requires that the programmer label each argument.

§Example

let t : Art<usize> =
  thunk!([ Some(name_unit()) ]?
    |x:usize,y:usize|{ if x > y { x } else { y }};
     x:10,   y:20   );

assert_eq!(get!(t), 20);

More examples of thunk! macro

§Use `force_map` for more precise dependencies

Suppose that we want to project only one field of type A from a pair within an Art<(A,B)>. If the field of type B changes, our observation of the A field will not be affected.

Below, we show that using force_map prunes the dirtying phase of change propagation. Doing so means that computations that would otherwise be dirty and cleaned via re-execution are never diritied in the first place. We show a simple example of projecting a pair.

To observe this fact, this test traces the engine, counts the number of dirtying steps, and ensures that this count is zero, as expected.

// Trace the behavior of change propagation; ensure dirtying works as expected
reflect::dcg_reflect_begin();

let pair  = cell!((1234, 5678));
let pair1 = pair.clone();

let t = thunk![{
  // Project the first component of pair:
  let fst = force_map(&pair, |_,x| x.0);
  fst + 100
}];

// The output is `1234 + 100` = `1334`
assert_eq!(get!(t), 1334);

// Update the second component of the pair; the first is still 1234
set(&pair1, (1234, 8765));

// The output is still `1234 + 100` = `1334`
assert_eq!(get!(t), 1334);

// Assert that nothing was dirtied (due to using `force_map`)
let traces = reflect::dcg_reflect_end();
let counts = reflect::trace::trace_count(&traces, None);
assert_eq!(counts.dirty.0, 0);
assert_eq!(counts.dirty.1, 0);

§Nominal memoization

Adapton offers nominal memoization, which uses first-class names (each of type Name) to identify cached computations and data.

fn sum(x:usize, y:usize) -> usize {
    x + y
}

// create a memo entry, named `a`, that remembers that `sum(42,43) = 85`
let res1 : usize = get!(thunk!([a] sum; x:42, y:43));

Behind the scenes, the name a controls how and when the Adapton engine overwrites the cached computation of sum. As such, names permit patterns of programmatic cache eviction.

The macro memo! relies on programmer-supplied variable names in its macro expansion of these call sites, shown as x and y in the uses above. These can be chosen arbitrarily: So long as these symbols are distinct from one another, they can be any symbols, and need not actually match the formal argument names.

Example as Editor role For a simple illustration, we memoize several function calls to sum with different names and arguments. In real applications, the memoized function typically performs more work than summing two machine words. :)

// Optional: Traces what the engine does below (for diagnostics, testing, illustration)
reflect::dcg_reflect_begin();

// create a memo entry, named `a`, that remembers that `sum(42,43) = 85`
let res1 : usize = get!(thunk!([a] sum; x:42, y:43));

// same name `a`, same arguments (42, 43), Adapton reuses cached result
let res2 : usize = get!(thunk!([a] sum; x:42, y:43));

// different name `b`, same arguments (42, 43), Adapton re-computes `sum` for `b`
let res3 : usize = get!(thunk!([b] sum; x:42, y:43));

// same name `b`, different arguments, editor overwrites thunk `b` with new args
let res4 : usize = get!(thunk!([b] sum; x:55, y:66));

Below we confirm the following facts:

The Editor:
- allocated two thunks (a and b),
- allocated one thunk without changing it (a, with the same arguments)
- allocated one thunk by changing it (b, with different arguments)
The Archivist allocated nothing.

// Optional: Assert what happened above, in terms of analytical counts
let traces = reflect::dcg_reflect_end();
let counts = reflect::trace::trace_count(&traces, None);

// Editor allocated two thunks (`a` and `b`)
assert_eq!(counts.alloc_fresh.0, 2);

// Editor allocated one thunk without changing it (`a`, with same args)
assert_eq!(counts.alloc_nochange.0, 1);

// Editor allocated one thunk by changing it (`b`, different args)
assert_eq!(counts.alloc_change.0, 1);

// Archivist allocated nothing
assert_eq!(counts.alloc_fresh.1, 0);

§Nominal Cycles

In many settings, we explore structures that contain cycles, and it is useful to use Adapton’s DCG mechanism to detect such cycles.

§Example problem: Recursive computation over a directed graph

As a tiny example, consider the following graph, defined as a table of adjacencies:

// Node | Adjacency pair
//      | (two outgoing edges to other nodes):
// -----+-------------------------------------
// 0    | (1, 0)
// 1    | (2, 3)
// 2    | (3, 0)
// 3    | (3, 1)
// 4    | (2, 5)
// 5    | (5, 4)

This is a small arbitrary directed graph, and it has several cycles (e.g., 0 --> 0, 3 --> 3, 0 --> 1 --> 2 --> 0). It also has distinct strongly-connected components (SCCs), e.g., the one involving 0 versus the one involving 4.

Problem statement: Suppose that we wish to explore this graph, to build a list (or Vec) with all of the edges that it contains.

Desired solution program: Consider the simple (naive) recursive exploration logic, defined as explore_rec below. The problems with this logic are that

Repeated work: explore_rec re-explores some sub-graphs multiple times, and
Divergence: explore_rec diverges on graphs with cycles.

To address the first problem, we can leverage the DCG, which performs function caching. To address the second problem, the algorithm needs a mechanism to detect cycles.

In terms of DCG evaluation, we can detect a cycle if we can remember and check whether we are “currently” visiting the node (on the recursive call stack) before we evaluate a node recursively.

Regardless of how we detect the cycle, we wish to do something different (other than recur).

§DCG cycles: Detection and valuation

Rather than implement this cycle-detection mechanism directly, we can use Adapton’s DCG, which operates behind the scenes. Specifically, we can use the engine operation force_cycle to specify a “cycle value” for the result of a thunk t when t is forcing itself, or when t is forcing another thunk s that transitively forces t.

In either case, the force operation that forms the cycle in the DCG evaluates to this programmer-specified cycle value, rather than diverging, or using the cached value at the thunk, which generally is not sound (e.g., it may be stale, from a prior run).

§Example cycle valuation

Notice that in explore below, we use get!(_, vec![]) on at and bt instead of get!(_). This macro uses force_cycle in its expansion. The empty vector gives the cycle value for when this force forms a cycle in the DCG.

// Define the graph, following the table above
fn adjs (n:usize) -> (usize, usize) {
    match n {
        0 => (1, 0),
        1 => (2, 3),
        2 => (3, 0),
        3 => (3, 1),
        4 => (2, 5),
        5 => (5, 4),
        _ => unimplemented!()
    }
}

// This version will diverge on all of the cycles (e.g., 3 --> 3)
#[warn(unconditional_recursion)]
fn explore_rec(cur_n:usize) -> Vec<usize> {
    let (a,b) = adjs(cur_n);
    let mut av = explore_rec(a);
    let mut bv = explore_rec(b);
    let mut res = vec![cur_n];
    res.append(&mut av);
    res.append(&mut bv);
    res
}

// This version will not diverge; it gives an empty vector value
// as "cycle output" when it performs each `get!`.  Hence, when
// Adapton detects a cycle, it will not re-force this thunk
// cyclicly, but rather return this predetermined "cycle output"
// value. For non-cyclic calls, the `get!` ignores this value, and
// works in the usual way.
fn explore(cur_n:usize) -> Vec<usize> {
    let (a,b) = adjs(cur_n);
    let at = explore_thunk(a);
    let bt = explore_thunk(b);
    let mut av = get!(at, vec![]);
    let mut bv = get!(bt, vec![]);
    let mut res = vec![cur_n];
    res.append(&mut av);
    res.append(&mut bv);
    res
}
fn explore_thunk(cur_n:usize) -> Art<Vec<usize>> {
    thunk!([Some(name_of_usize(cur_n))]? explore ; n:cur_n)
}

adapton::engine::manage::init_dcg();
assert_eq!(get!(explore_thunk(0)), vec![0,1,2,3,3])

§Nominal Firewalls

Nominal firewalls use nominal allocation to dirty the DCG incrementally, while change propagation cleans it.

In some situations (Run 2, below), these firewalls prevent dirtying from cascading, leading to finer-grained dependency tracking, and more incremental reuse. Thanks to @nikomatsakis for suggesting the term “firewall” in this context.

First, consider this graph, as Rust code (graph picture below):

§Example: nominal firewall

fn demand_graph(a: Art<i32>) -> String {
    let_memo!{
      d =(f)= {
        let a = a.clone();
        let_memo!{ b =(g)={ let x = get!(a); cell!([b] x * x) };
                   c =(h)={ format!("{:?}", get!(b)) };
                   c }};
      d }
}

The use of let_memo! is convenient sugar for thunk! and force. This code induces DCGs with the following structure:

/*                                             +---- Legend ------------------+
cell a                                         | [ 2 ]   ref cell holding 2   |
[ 2 ]            "Nominal                      |  (g)    thunk named 'g'      |
  ^               firewall"                    | ---->   force/observe edge   |
  | force            |                         | --->>   allocation edge      |
  | 2               \|/                        +------------------------------+
  |                  `
  |   g allocs b    cell    g forces b          When cell a changes, g is dirty, h is not;
  |   to hold 4      b      observes 4          in this sense, cell b _firewalls_ h from g:
 (g)------------->>[ 4 ]<--------------(h)  <~~ note that h does not observe cell a, or g.
  ^                                     ^
  | f forces g                          | f forces h,
  | g returns cell b                    | returns String "4"
  |                                     |
 (f)------------------------------------+
  ^
  | force f,
  | returns String "4"
  |
(demand_graph(a))                                                                        */

In this graph, the ref cell b acts as the “firewall”.

Below, we show a particular input change for cell a where a subcomputation h is never dirtied nor cleaned by change propagation (input change 2 to -2). We show another change to the same input where this subcomputation h is eventually dirtied and cleaned by Adapton, though not immediately (input change -2 to 3).

Here’s the Rust code for generating this DCG, and these changes to its input cell, named "a":

// 1. Initialize input cell "a" to hold 2, and do the computation illustrated above:
assert_eq!(demand_graph(let_cell!{a = 2; a}), "4".to_string());

// 2. Change input cell "a" to hold -2, and do the computation illustrated above:
assert_eq!(demand_graph(let_cell!{a = -2; a}), "4".to_string());

// 3. Change input cell "a" to hold 3, and do the computation illustrated above:
assert_eq!(demand_graph(let_cell!{a = 3; a}),  "9".to_string());

Run 1. In the first computation, the input cell a holds 2, and the final result is "4".

Run 2. When the input cell a changes, e.g., from 2 to -2, thunks f and g are dirtied. Thunk g is dirty because it observes the changed input. Thunk f is dirty because it demanded (observed) the output of thunk g in the extent of its own computation.

Importantly, thunk h is not immediately dirtied when cell a changes. In a sense, cell a is an indirect (“transitive”) input to thunk h. This fact may suggest that when cell a is changed from 2 to -2, we should dirty thunk h immediately. However, thunk h is related to this input only by reading ref cell b.

Rather, when the editor re-demands thunk f, Adapton will necessarily perform a cleaning process (aka, “change propagation”), re-executing g, its immediate dependent, which is dirty. Since thunk g merely squares its input, and 2 and -2 both square to 4, the output of thunk g will not change in this case. Consequently, the observers of cell b, which holds this output, will not be dirtied or re-executed. In this case, thunk h is this observer. In situations like these, Adapton’s dirtying + cleaning algorithms do not dirty nor clean thunk h.

In sum, under this change, after f is re-demanded, the cleaning process will first re-execute g, the immediate observer of cell a. Thunk g will again allocate cell b to hold 4, the same value as before. It also yields this same cell pointer (to cell b). Consequently, thunk f is not re-executed, and is cleaned. Meanwhile, the outgoing (dependency) edges thunk of h are never dirtied. Effectively, the work of h is reused from cache as well.

Alternatively, if we had placed the code for format!("{:?}",get!(b)) in thunk f, Adapton would have re-executed this step when a changes from 2 to -2: It would be dirtied when a changes, since it directly observes g, which directly observes cell a.

Run 3. For some other change, e.g., from 2 to 3, thunk h would eventually will be

dirtied, when f redemands g, which will overwrite cell b with 9,
and cleaned, when f re-demands h, which will format! a new String of "9".

§`let_memo!` example

The use of let_memo! macro above expands as follows:

fn demand_graph__mid_macro_expansion(a: Art<i32>) -> String {
    let f = thunk!([f]{
              let a = a.clone();
              let g = thunk!([g]{ let x = get!(a);
                                  cell!([b] x * x) });
              let b = force(&g);
              let h = thunk!([h]{ let x = get!(b);
                                  format!("{:?}", x) });
              let c = force(&h);
              c });
    let d = force(&f);
    d
};

§Incremental sequences

A level tree consists of a binary tree with levels that decrease monotonically along each path to its leaves.

Here, we implement incremental level trees by including Names and Arts in the tree structure, with two additional constructors for the recursive type, Rec<X>:

use std::fmt::Debug;
use std::hash::Hash;

#[derive(Clone,PartialEq,Eq,Debug,Hash)]
enum Rec<X> {
    Bin(BinCons<X>),
    Leaf(LeafCons<X>),
    Name(NameCons<X>),
    Art(Art<Rec<X>>),
}

#[derive(Clone,PartialEq,Eq,Debug,Hash)]
struct LeafCons<X> {
    elms:Vec<X>,
}

#[derive(Clone,PartialEq,Eq,Debug,Hash)]
struct BinCons<X> {
    level: u32,
    recl:Box<Rec<X>>,
    recr:Box<Rec<X>>
}

#[derive(Clone,PartialEq,Eq,Debug,Hash)]
struct NameCons<X> {
    level:u32,
    name:Name,
    rec:Box<Rec<X>>,
}

§Example: Nominal memoization and recursion

Introduction forms:

impl<X:'static+Clone+PartialEq+Eq+Debug+Hash>
    Rec<X> {

pub fn leaf(xs:Vec<X>) -> Self {
    Rec::Leaf(LeafCons{elms:xs})
}
pub fn bin(lev:u32, l:Self, r:Self) -> Self {
    Rec::Bin(BinCons{level:lev,recl:Box::new(l),recr:Box::new(r)})
}
pub fn name(lev:u32, n:Name, r:Self) -> Self {
    Rec::Name(NameCons{level:lev,name:n, rec:Box::new(r)})
}
fn art(a:Art<Rec<X>>) -> Self {
    Rec::Art(a)
}

Elimination forms: Folds use memo! to create and force thunks:

pub fn fold_monoid<B:'static+Clone+PartialEq+Eq+Debug+Hash>
   (t:Rec<X>, z:X, b:B,
    bin:fn(B,X,X)->X,
    art:fn(Art<X>,X)->X)
   -> X
{
  fn m_leaf<B:Clone,X>(m:(B,fn(B,X,X)->X,X), elms:Vec<X>) -> X {
     // ...
  }
  fn m_bin<B,X>(_n:Option<Name>, m:(B,fn(B,X,X)->X,X), _lev:u32, l:X, r:X) -> X {
      m.1(m.0, l, r)
  }
  Self::fold_up_namebin::<(B,fn(B,X,X)->X,X),
                          (B,fn(B,X,X)->X,X),X> (t, (b.clone(),bin,z.clone()), m_leaf,
                                                 None, (b,bin,z), m_bin, art)
}

fn fold_up_namebin
   <L:'static+Clone+PartialEq+Eq+Debug+Hash,
    B:'static+Clone+PartialEq+Eq+Debug+Hash,
    R:'static+Clone+PartialEq+Eq+Debug+Hash>
   (t:Rec<X>,
    l:L, leaf:fn(L,Vec<X>)->R,
    n:Option<Name>, b:B,
    namebin:fn(Option<Name>,B,u32,R,R)->R,
    art:fn(Art<R>,R)->R)
   -> R
{
  match t {
    Rec::Art(a) => Self::fold_up_namebin(get!(a), l, leaf, n, b, namebin, art),
    Rec::Leaf(leafcons) => leaf(l, leafcons.elms),
    Rec::Bin(bincons)   => {
        let (n1,n2) = forko!(n.clone());
        let r1 = memo!([n1]? Self::fold_up_namebin;
                       t:*bincons.recl,
                       l:l.clone(), leaf:leaf, n:None, b:b.clone(), namebin:namebin, art:art);
        let r1 = art(r1.0,r1.1);
        let r2 = memo!([n2]? Self::fold_up_namebin;
                       t:*bincons.recr,
                       l:l.clone(), leaf:leaf, n:None, b:b.clone(), namebin:namebin, art:art);
        let r2 = art(r2.0,r2.1);
        namebin(n, b, bincons.level, r1, r2)
    }
    Rec::Name(namecons) => {
        Self::fold_up_namebin(
            *namecons.rec,
            l, leaf, Some(namecons.name), b, namebin, art
        )
    }
  }
}

§Background: Incremental Computing with Names

We explain the role of names in incremental computing.

§Pointer locations in incremental computing

Suppose that we have a program that we wish to run repeatedly on similar (but changing) inputs, and that this program constructs a dynamic data structure as output. To cache this computation, including its output, we generally require caching some of its function calls, their results, and whatever allocations are relevant to represent these results, including the final output structure. Furthermore, to quickly test for input and output changes (in O(1) time per “change”) we would like to store allocate input and output, and use allocated pointer locations (globally-unique “names”) to compare structures, giving a cheap, conservative approximation of structural equality.

§Deterministic allocation

The first role of explicit names for incremental computing concerns deterministic pointer allocation, which permits us to give a meaningful definition to cached allocation. To understand this role, consider these two evaluation rules:

// l ∉ dom(σ)                                    n ∉ dom(σ)
// ---------------------------- :: alloc_1       ------------------------------- :: alloc_2
// σ; cell(v) ⇓ σ{l↦v}; ref l                    σ; cell[n](v) ⇓ σ{n↦v}; ref n

Each rule is of the judgement form σ1; e ⇓ σ2; v, where σ1 and σ2 are stores that map pointers to thunks and values, and e is an expression to evaluate, and v is its valuation.

The left rule is conventional: it allocates a value v at a store location l; because the program does not determine l, the implementor of this rule has the freedom to choose l any way that they wish. Consequently, this program is not deterministic, and not a function. Hence, it is not immediately obvious what it means to cache this kind of dynamic allocation using a technique like function caching, or techniques based on it.

To address this question, the programmer can determine a name n for the value v as in the right rule. The point of this version is to expose the naming choice directly to the programmer.

§Structural names

In some systems, the programmer chooses this name as the hash value of value v. This naming style is often called “hash-consing”. We refer to it as structural naming, since by using it, the name of each ref cell reflects the entire structure of that cell’s content. (Structural hashing approach is closely related to Merkle trees, the basis for revision-control systems like git.)

§Independent names

By contrast, in a nominal incremental system, the programmer generally chooses n to be related to the evaluation context of using v, and often, to be independent of the value v itself. We give one example of such a naming strategy below.

§Nominal independence

Names augment programs to permit memoization and change propagation to exploit independence among dynamic dependencies. Specifically, the name value n is (generally) unrelated to the content value v. In many incremental applications, its role is analogous to that of location l in the left rule, where l is only related to v by the final store. When pointer name n is independent of pointer content v, we say this name, via the store, affords the program nominal independence.

Suppose that in a subsequent incremental run, value v changes to v2 at name n. The pointer name n localizes this change, preventing any larger structure that contains cell n from itself having a changed identity. By contrast, consider the case of structural naming, which lacks nominal indirection: by virtue of being determined by the value v, the allocated name n must change to n2 when v changes to v2. Structural naming is deterministic, but lacks nominal independence, by definition.

§Simple example of nominal independence

The independence afforded by nominal indirection is critical in many incremental programs. As a simple illustrative example, consider rev, which recursively reverses a list that, after being reversed, undergoes incremental insertions and removals.

// rev : List -> List -> List
// rev l r = match l with
//  | Nil       => r
//  | Cons(h,t) =>
//     memo(rev !t (Cons(h,r)))

The function rev reverses a list of Cons cells, using an accumulator value r. To incrementalize the code for rev, in the Cons case, we memoize the recursive call to rev, which involves matching its arguments with those of cached calls.

Problematically, if we do not introduce any indirection for it, the accumulator Cons(h,r) will contain any incremental changes to head value h, as well as any changes in the prefix of the input list (now reversed in the previous accumulator value r). This is a problem for memoization because, without indirection in this accumulator list, such changes will repeatedly prevent us from memo-matching the recursive call. Consequently, change propagation will re-evaluate all the calls that follow the position of an insertion or removal: This change is recorded in the accumulator, which has changed structurally.

To address this issue, which is an example of a general pattern (c.f. the output accumulators of quicksort and quickhull), past researchers suggest that we introduce nominal cells into the accumulator, each allocated with a name associated with their corresponding input Cons cell. In place of “names”, prior work variously used the terms (allocation) keys\cite{AcarThesis,Hammer08,AcarLeyWild09} and indices\cite{Acar06,Acar06ML}, but the core idea is the same.

// | Cons(n,h,t) =>
//    let rr = ref[n](r) in
//    memo(rev !t (Cons(h,rr)))

In this updated version, each name n localizes any change to the accumulator argument r via nominal indirection. When and if a later part of the program consumes the output in ref cell rr, the system will process any changes associated with this accumulator; they may be relevant later, but they are not directly relevant for reversing the tail !t in cell t: The body of rev never inspects r, it merely uses it to construct its output, for the Nil base case.

In summary, this example illustrate a general principle: Nominal indirection augments programs to permit memoization and change propagation to exploit dynamic independence. Specifically, we exploit the independence of the steps that reverse the pointers of a linked list.

Modules§

catalog
Experimental collections, including those for sequences and sets. (See also: The IODyn crate)
engine
Adapton’s core calculus, implemented as a runtime library. We implement two versions of this interface, which we refer to as engines: The naive engine and the DCG engine, implemented based on the algorithms from the Adapton papers.
macros
Macros to make using the engine module’s interface more ergonomic.
parse_val
Parses the output of Rust Debug strings into reflected values of type Val. (See engine::reflect module).
reflect
Reflects the DCG engine, including both the effects of the programs running in it, and the internal effects of the engine cleaning and dirtying the DCG. For the latter effects, see the trace module.

Macros§

cell
Convenience wrappers for engine::cell.
fork
Wrappers for engine::fork_name.
forko
Optional name forking.
get
Convenience wrapper for engine::force
let_cell
Let-bind a nominal ref cell via cell, using the let-bound variable identifier as its name. Permits sequences of bindings.
let_memo
Let-bind a nominal thunk, force it, and let-bind its result. Permits sequences of bindings.
let_thunk
Let-bind a nominal thunk via thunk!, without forcing it. Permits sequences of bindings.
memo
Wrappers for creating and forcing thunks (engine::thunk and engine::force).
thunk
Wrappers for engine::thunk.

Crate adaptonCopy item path

§Adapton for Rust

§Programming model

§Resources

§Background

§Why Rust?

§Adapton programming model

§Start the DCG engine

§Create incremental cells

§Implicit cell names

§Naming strategy: Global counter

§Explicitly named cells

§Names via Rust “identifiers”

§Optional Names

§Observe Arts

§Mutate input cells

§Demand-driven change propagation

§Switching

§Memoization

§Optional name version

§Example

§Create thunks

§Example

§Use force_map for more precise dependencies

§Nominal memoization

§Nominal Cycles

§Example problem: Recursive computation over a directed graph

§DCG cycles: Detection and valuation

§Example cycle valuation

§Nominal Firewalls

§Example: nominal firewall

§let_memo! example

§Incremental sequences

§Example: Nominal memoization and recursion

§Background: Incremental Computing with Names

§Pointer locations in incremental computing

§Deterministic allocation

§Structural names

§Independent names

§Nominal independence

§Simple example of nominal independence

Modules§

Macros§

Crate adapton

§Implicit `cell` names

§Explicitly named `cell`s

§Optional `Name`s

§Observe `Art`s

§Use `force_map` for more precise dependencies

§`let_memo!` example